ABC045
ABC045
[ABC045A] 台形
题面翻译
一个梯形,给出上底a,下底b,高h的长度,求它的面积~~~
题目描述
上底の長さが $ a $、下底の長さが $ b $、高さが $ h $ の台形があります。
台形の例
この台形の面積を求めてください。
输入格式
入力は以下の形式で標準入力から与えられる。
$ a $ $ b $ $ h $
输出格式
台形の面積を整数で出力せよ。面積が整数になることは保障されている。
样例 #1
样例输入 #1
4
2样例输出 #1
样例 #2
样例输入 #2
4
4样例输出 #2
提示
制約
- $ 1 a 100 $
- $ 1 b 100 $
- $ 1 h 100 $
- 入力で与えられる値はすべて整数
- $ h $ は偶数
Sample Explanation 1
上底の長さ $ 3 $、下底の長さ $ 4 $、高さ $ 2 $ の台形の面積は、 $ (3+4)×2/2 = 7 $ です。
Sample Explanation 2
この例で与えられるのは平行四辺形ですが、平行四辺形も台形です。
思路
直接模拟即可
|
[ABC045B] 3人でカードゲームイージー
题面翻译
题面描述
Alice、Bob 和 Charlie 在玩 Card Game for Three。
- 开始时,每名玩家有一叠由卡牌组成的牌堆。每张牌上有一个字母 \(\texttt a, \texttt b\) 或 \(\texttt c\)。 卡牌的顺序不能被改变。
- Alice 先开始游戏。
- 玩家的牌堆中至少有一张牌,当前玩家从牌堆顶抽出一张牌,这张牌代表的玩家进行下一回合(\(\texttt a\) 代表 Alice,\(\texttt c\) 代表 Bob,\(\texttt c\) 代表 Charlie)。
- 从左往右抽牌(牌堆顶在左边)。
- 如果当前玩家的牌堆空了,游戏结束,这名玩家胜利。
你得到了每名玩家最初的牌堆 \(S_a, S_b, S_c\),求出胜者。
数据范围
对于 \(100 \%\) 的数据,保证 \(1 \leq |S_a|, |S_b|, |S_c| \leq 100\) 且 \(S_a, S_b, S_c\) 仅由 \(\texttt{abc}\) 三个小写拉丁字母组成。
题目描述
A さん、B さん、C さんの $ 3 $ 人が以下のようなカードゲームをプレイしています。
- 最初、$ 3 $ 人はそれぞれ
a、b、cいずれかの文字が書かれたカードを、何枚か持っている。これらは入力で与えられた順番に持っており、途中で並べ替えたりしない。- $ A $ さんのターンから始まる。
- 現在自分のターンである人がカードを $ 1 $ 枚以上持っているならば、そのうち先頭のカードを捨てる。その後、捨てられたカードに書かれているアルファベットと同じ名前の人 (例えば、カードに
aと書かれていたならば A さん) のターンとなる。- 現在自分のターンである人がカードを $ 1 $ 枚も持っていないならば、その人がゲームの勝者となり、ゲームは終了する。
$ 3 $ 人が最初に持っているカードがそれぞれ先頭から順に与えられます。 具体的には、文字列 $ S_A \(、\) S_B \(、\) S_C $ が与えられます。文字列 $ S_A $ の $ i $ 文字目 ( $ 1 i |S_A| $ ) に書かれている文字が、A さんの持っている中で先頭から $ i $ 番目のカードに 書かれている文字です。文字列 $ S_B $、 $ S_C $ についても同様です。
最終的に誰がこのゲームの勝者となるかを求めてください。
输入格式
入力は以下の形式で標準入力から与えられる。
$ S_A $ $ S_B $ $ S_C $
输出格式
A さんが勝つなら
A、B さんが勝つならB、C さんが勝つならCと出力せよ。样例 #1
样例输入 #1
accc
ca样例输出 #1
样例 #2
样例输入 #2
aacb
bccc样例输出 #2
提示
制約
- $ 1 S_A 100 $
- $ 1 S_B 100 $
- $ 1 S_C 100 $
- $ S_A \(、\) S_B \(、\) S_C $ に含まれる文字はそれぞれ
a、b、cのいずれかSample Explanation 1
ゲームは以下のように進行します。 - A さんが、持っている中で最初のカード
aを捨てる。次は A さんの番となる。 - A さんが、持っている中で最初のカードcを捨てる。次は C さんの番となる。 - C さんが、持っている中で最初のカードcを捨てる。次は C さんの番となる。 - C さんが、持っている中で最初のカードaを捨てる。次は A さんの番となる。 - A さんが、持っている中で最初のカードaを捨てる。次は A さんの番となる。 - A さんはもう持っているカードがない。よって A さんの勝利となり、ゲームは終了する。
思路
其实是到模拟题,感觉有点像链表。
用\(p\)代表每个字符串对应的指针,不断按照题意进行移动操作,直到当前牌堆空为止。
思路参考自[题解 AT2066 ABC045B] 3人でカードゲームイージー / Card Game for Three (ABC Edit) - 洛谷专栏 (luogu.com.cn)
|
[ABC045C] たくさんの数式
题面翻译
Translated by aoweiyin
题意翻译
有一个仅由字符
1到9构成的字符串\(S(1\leq |S|\leq 10)\),让你在中间添加+,使其变成一个加式。求所有方案的和值(详见样例解释)。样例解释1:
输入
125,输出176.有4种:
- 125
- 1+25=26
- 12+5=17
- 1+2+5=8
题目描述
1以上9以下の数字のみからなる文字列 $ S $ が与えられます。 この文字列の中で、あなたはこれら文字と文字の間のうち、いくつかの場所に+を入れることができます。 一つも入れなくてもかまいません。 ただし、+が連続してはいけません。このようにして出来る全ての文字列を数式とみなし、和を計算することができます。
ありうる全ての数式の値を計算し、その合計を出力してください。
输入格式
入力は以下の形式で標準入力から与えられる。
$ S $
输出格式
ありうる全ての数式の値の総和を $ 1 $ 行に出力せよ。
样例 #1
样例输入 #1
样例输出 #1
样例 #2
样例输入 #2
样例输出 #2
提示
制約
- $ 1|S| $
- $ S $ に含まれる文字は全て
1〜9の数字Sample Explanation 1
考えられる数式としては、
125、1+25、12+5、1+2+5の $ 4 $ 通りがあります。それぞれの数式を計算すると、 - $ 125 $ - $ 1+25=26 $ - $ 12+5=17 $ - $ 1+2+5=8 $ となり、これらの総和は $ 125+26+17+8=176 $ となります。
思路
用DFS就可以解决了,将每一位进行拆分,用数组记录下来。
\(+\)的插入有两种情况:
DFS数字的每一位,可以将这一位与上一个数进行结合,也可以在中间加上一个\(+\),具体看代码。
|
其实有更好的方法:看看这篇文章
[题解 AT2067 【ARC061A] たくさんの数式 / Many Formulas】 - 洛谷专栏 (luogu.com.cn)
[ABC045D] すぬけ君の塗り絵
题面翻译
给定一个 \(H\) 行 \(W\) 列的矩形,再给定矩形上 \(N\) 个黑格子的坐标。对于每个 \(0\le j\le9\) ,求出有多少个 \(3\times3\) 的子矩阵包含有恰好 \(j\) 个黑格子。
题目描述
縦 $ H $ 行、横 $ W $ 列のマス目からなる盤があります。最初、どのマス目も白く塗られています。
すぬけ君が、このうち $ N $ マスを黒く塗りつぶしました。$ i $ 回目 ( $ 1 i N $ ) に塗りつぶしたのは、 上から $ a_i $ 行目で左から $ b_i $ 列目のマスでした。
すぬけ君がマス目を塗りつぶした後の盤の状態について、以下のものの個数を計算してください。
- 各整数 $ j $ ( $ 0 j 9 $ ) について、盤の中に完全に含まれるすべての $ 3 $ 行 $ 3 $ 列の連続するマス目のうち、黒いマスがちょうど $ j $ 個あるもの。
输入格式
入力は以下の形式で標準入力から与えられる。
$ H $ $ W $ $ N $ $ a_1 $ $ b_1 $ : $ a_N $ $ b_N $
输出格式
出力は $ 10 $ 行からなる。 $ j+1 $ 行目 ( $ 0 j 9 $ ) には、盤の中に完全に含まれるすべての $ 3 $ 行 $ 3 $ 列の連続するマス目のうち、黒いマスがちょうど $ j $ 個あるものの 総数を出力せよ。
样例 #1
样例输入 #1
1 1
1 4
1 5
2 3
3 1
3 2
3 4
4 4样例输出 #1
0
0
2
4
0
0
0
0
0样例 #2
样例输入 #2
1 1
1 4
1 9
2 5
3 10
4 2
4 7
5 9
6 4
6 6
6 7
7 1
7 3
7 7
8 1
8 5
8 10
9 2
10 4
10 9样例输出 #2
26
22
10
2
0
0
0
0
0样例 #3
样例输入 #3
样例输出 #3
0
0
0
0
0
0
0
0
0提示
制約
- $ 3 H 10^9 $
- $ 3 W 10^9 $
- $ 0 N min(10^5,H×W) $
- $ 1 a_i H $ $ (1 i N) $
- $ 1 b_i W $ $ (1 i N) $
- $ (a_i, b_i) (a_j, b_j) $ $ (i j) $
Sample Explanation 1
 この盤に含まれる $ 3×3 $ の正方形は全部で $ 6 $ 個ありますが、これらのうち $ 2 $ 個の内部には黒いマスが $ 3 $ 個、残りの $ 4 $ 個の内部には黒いマスが $ 4 $ 個含まれています。
思路
思路参考自AT2068题解 - 洛谷专栏 (luogu.com.cn)
直接开数组模拟肯定喜提TLE,MLE。
这时候就要想到贡献法,就是每输入一个格子,计算它对包含它的九宫格的贡献(记得判边界)
所以我们只需维护一个答案数组,每次计算新格子对它的影响就行了
但是,又有个新问题:如何记录新加进来的格子所在的九宫格原来黑格子的个数呢?
显然我们可以用 map 来解决,用它来维护以\(x,y\)为中心的九宫格黑格子个数
完结撒花!
|

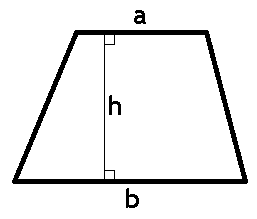 台形の例
台形の例




