前缀和、差分、离散化

【深进1.例1】求区间和

【深进1.例1】求区间和

题目描述

给定 \(n\) 个正整数组成的数列 \(a_1, a_2, \cdots, a_n\) 和 \(m\) 个区间 \([l_i,r_i]\)，分别求这 \(m\) 个区间的区间和。

对于所有测试数据，\(n,m\le10^5,a_i\le 10^4\)

输入格式

第一行，为一个正整数 \(n\) 。

第二行，为 \(n\) 个正整数 \(a_1,a_2, \cdots ,a_n\)

第三行，为一个正整数 \(m\) 。

接下来 \(m\) 行，每行为两个正整数 \(l_i,r_i\) ，满足\(1\le l_i\le r_i\le n\)

输出格式

共 \(m\) 行。

第 \(i\) 行为第 \(i\) 组答案的询问。

样例 #1

样例输入 #1

4 4 3 2 1 2 1 4 2 3

样例输出 #1

10 5

提示

样例解释：第 \(1\) 到第 \(4\) 个数加起来和为 \(10\)。第 \(2\) 个数到第 \(3\) 个数加起来和为 \(5\)。

对于 \(50 \%\) 的数据：\(n,m\le 1000\)；

对于 \(100 \%\) 的数据：\(1 \le n, m\le 10^5\)，\(1 \le a_i\le 10^4\)

思路分析

简单的前缀和板子，不多说。 ## AC代码

#include<iostream>
using namespace std;
using ll =unsigned long long;
ll n, m;
ll a[200000];
ll pre[200000], sum[200000];
int main() {
	cin >> n;
	for (ll i = 1; i <= n; i++) {
		cin >> a[i];
		pre[i] = a[i] + pre[i - 1];
	}
	cin >> m;
	for (ll i = 1; i <= m; i++) {
		ll l = 0, r = 0;
		cin >> l >> r;
		sum[i] = pre[r] - pre[l - 1];
	}
	for (ll i = 1; i <= m; i++) {
		cout << sum[i] << endl;
	}
	return 0;
}

最大加权矩形

题目描述

为了更好的备战 NOIP2013，电脑组的几个女孩子 LYQ,ZSC,ZHQ 认为，我们不光需要机房，我们还需要运动，于是就决定找校长申请一块电脑组的课余运动场地，听说她们都是电脑组的高手，校长没有马上答应他们，而是先给她们出了一道数学题，并且告诉她们：你们能获得的运动场地的面积就是你们能找到的这个最大的数字。

校长先给他们一个 \(n\times n\) 矩阵。要求矩阵中最大加权矩形，即矩阵的每一个元素都有一权值，权值定义在整数集上。从中找一矩形，矩形大小无限制，是其中包含的所有元素的和最大 。矩阵的每个元素属于 \([-127,127]\) ,例如

 0 –2 –7  0 
 9  2 –6  2
-4  1 –4  1 
-1  8  0 –2

在左下角：

9  2
-4  1
-1  8

和为 \(15\)。

几个女孩子有点犯难了，于是就找到了电脑组精打细算的 HZH，TZY 小朋友帮忙计算，但是遗憾的是他们的答案都不一样，涉及土地的事情我们可不能含糊，你能帮忙计算出校长所给的矩形中加权和最大的矩形吗？

输入格式

第一行：\(n\)，接下来是 \(n\) 行 \(n\) 列的矩阵。

输出格式

最大矩形（子矩阵）的和。

样例 #1

样例输入 #1

4
0 -2 -7 0
 9 2 -6 2
-4 1 -4  1 
-1 8  0 -2

样例输出 #1

15

提示

\(1 \leq n\le 120\) 其实是二维前缀和的板子，这里给出几份代码，看看不同的思路（大多都是细节上处理的方法不同）。

AC代码

CODE1

#include<iostream>
#include<algorithm>
using namespace std;
using ll = long long;
int n, ans = -99999999;
int squ[130][130];
int sum[130][130];
int lin[130][130];
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> squ[i][j];
			//lin[i][j]表示的是第i行前j个（其实也就是第j列）数字的和
			lin[i][j] = lin[i][j - 1] + squ[i][j];
			//sum[i][j]表示的是以第1行第1个数字为左上角，以第i行第j个数字为右下角的矩形的面积。
			sum[i][j] = sum[i - 1][j] + lin[i][j];
		}
	}
	//分别枚举左上角的坐标(x1,y1)和右下角(x2,y2)的坐标。
	for (int x1 = 1; x1 <= n; x1++) {
		for (int y1 = 1; y1 <= n; y1++) {
			for (int x2 = 1; x2 <= n; x2++) {
				for (int y2 = 1; y2 <= n; y2++) {
					if (x2 < x1||y2<y1) {
						continue;
					}
					ans = max(ans, sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] +sum[x1-1][y1-1]);
				}
			}
		}
	}
	cout << ans;
	return 0;
}

可能有人对\(sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] +sum[x1-1][y1-1]\)为什么是以\((x_1,y_1)\)为左上角，以\((x_2,y_2)\)为右下角的矩形的面积有点疑惑。画个图解释一下： 这下应该能看懂了吧qwq。

CODE2

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
int a[125][125],mat[125][125];
int query(int i,int j,int k,int m){
    //还是跟上面的操作一样
    return mat[k][m]-mat[k][j-1]-mat[i-1][m]+mat[i-1][j-1];
}
int main(){
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>a[i][j];
            //预处理出以(i,j)为右下角的矩形的面积，画画图就懂了
            mat[i][j]=mat[i-1][j]+mat[i][j-1]-mat[i-1][j-1]+a[i][j];
        }
    }
    int ans=-1e9;
    //枚举左上角(i,j)，右下角(k,m)
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            //注意k>=i,m>=j
            for(int k=i;k<=n;k++){
                for(int m=j;m<=n;m++){
                    ans=max(ans,query(i,j,k,m));
                }
            }
        }
    }
    cout<<ans<<"\n";
    return 0;
}

CODE3

实际上是在枚举时优化了一下，降低时间复杂度。

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
int a[125][125],mat[125][125];
int query(int i,int j,int k,int m){
    return mat[k][m]-mat[k][j-1]-mat[i-1][m]+mat[i-1][j-1];
}
int main(){
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>a[i][j];
            mat[i][j]=mat[i-1][j]+mat[i][j-1]-mat[i-1][j-1]+a[i][j];
        }
    }
    int ans=-1e9,sum;
    //这里改成了枚举矩形的上下边i与j
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j++){
            sum=0;
            //k枚举的是第几列，从左往右扫描每一列的面积，并加到sum中
            for(int k=1;k<=n;k++){
                sum+=query(i,k,j,k);
                //如果sum>ans，说明在以i行为上界，j行为下界的，并且右界限为k的构成的连续矩形面积（即sum）更大，更新ans
                if(sum>ans)ans=sum;
                //如果sum<0，那么只能另开一段，置sum为0
                if(sum<0)sum=0;
            }
        }
    }
    cout<<ans<<"\n";
    return 0;
}

或者可以理解成是矩阵压缩，可以看看题解的第一篇，本质其实是一样的。 P1719 最大加权矩形

语文成绩

语文成绩

题目背景

语文考试结束了，成绩还是一如既往地有问题。

题目描述

语文老师总是写错成绩，所以当她修改成绩的时候，总是累得不行。她总是要一遍遍地给某些同学增加分数，又要注意最低分是多少。你能帮帮她吗？

输入格式

第一行有两个整数 \(n\)，\(p\)，代表学生数与增加分数的次数。

第二行有 \(n\) 个数，\(a_1 \sim a_n\)，代表各个学生的初始成绩。

接下来 \(p\) 行，每行有三个数，\(x\)，\(y\)，\(z\)，代表给第 \(x\) 个到第 \(y\) 个学生每人增加 \(z\) 分。

输出格式

输出仅一行，代表更改分数后，全班的最低分。

样例 #1

样例输入 #1

3 2 1 1 1 1 2 1 2 3 1

样例输出 #1

2

提示

对于 \(40\%\) 的数据，有 \(n \le 10^3\)。

对于 \(60\%\) 的数据，有 \(n \le 10^4\)。

对于 \(80\%\) 的数据，有 \(n \le 10^5\)。

对于 \(100\%\) 的数据，有 \(n \le 5\times 10^6\)，\(p \le n\)，学生初始成绩 $ \(，\)z $。

思路分析

差分的板子题，但是我经常忘记怎么操作了，贴上证明。 这里贴的是GoldenFishX大佬的博客，可以看看（大佬如果觉得侵权，联系我删除即可qwq）。 ## AC代码

#include<iostream>
using namespace std;
using ll = long long;
ll p, n, a[5000500], d[5000500];
ll x, y, z, ans=9999999999;
int main() {
	cin >> n >> p;
	for (ll i = 1; i <= n; i++) {
		cin >> a[i];
		//求出差分数组
		d[i] = a[i] - a[i - 1];
	}
	for (ll i = 1; i <= p; i++) {
		cin >> x >> y >> z;
		//上面讲得很清楚了
		d[x] += z;
		d[y + 1] -= z;
	}
	for (ll i = 1; i <= n; i++) {
	    //差分的性质：a[i]=d[i]+d[i-1]+d[i-2]+······+d[1]
		a[i] = a[i - 1] + d[i];
		ans = min(ans, a[i]);
	}
	cout << ans;
	return 0;
}

地毯

题目描述

在 \(n\times n\) 的格子上有 \(m\) 个地毯。

给出这些地毯的信息，问每个点被多少个地毯覆盖。

输入格式

第一行，两个正整数 \(n,m\)。意义如题所述。

接下来 \(m\) 行，每行两个坐标 \((x_1,y_1)\) 和 \((x_2,y_2)\)，代表一块地毯，左上角是 \((x_1,y_1)\)，右下角是 \((x_2,y_2)\)。

输出格式

输出 \(n\) 行，每行 \(n\) 个正整数。

第 \(i\) 行第 \(j\) 列的正整数表示 \((i,j)\) 这个格子被多少个地毯覆盖。

样例 #1

样例输入 #1

5 3
2 2 3 3
3 3 5 5
1 2 1 4

样例输出 #1

0 1 1 1 0
0 1 1 0 0
0 1 2 1 1
0 0 1 1 1
0 0 1 1 1

提示

样例解释

覆盖第一个地毯后：

\(0\)	\(0\)	\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(1\)	\(0\)	\(0\)
\(0\)	\(1\)	\(1\)	\(0\)	\(0\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)

覆盖第一、二个地毯后：

\(0\)	\(0\)	\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(1\)	\(0\)	\(0\)
\(0\)	\(1\)	\(2\)	\(1\)	\(1\)
\(0\)	\(0\)	\(1\)	\(1\)	\(1\)
\(0\)	\(0\)	\(1\)	\(1\)	\(1\)

覆盖所有地毯后：

\(0\)	\(1\)	\(1\)	\(1\)	\(0\)
\(0\)	\(1\)	\(1\)	\(0\)	\(0\)
\(0\)	\(1\)	\(2\)	\(1\)	\(1\)
\(0\)	\(0\)	\(1\)	\(1\)	\(1\)
\(0\)	\(0\)	\(1\)	\(1\)	\(1\)

---

数据范围

对于 \(20\%\) 的数据，有 \(n\le 50\)，\(m\le 100\)。

对于 \(100\%\) 的数据，有 \(n,m\le 1000\)。 ## 思路分析 这题其实可以暴力模拟水过去，但实际上正解是二维差分。（补学一下qwq）。 设数组\(a\)的差分数组为\(b\)，则： \[b[[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]\]. （偷懒了，直接贴书上的内容qwq）

在这里插入图片描述

可以看到(a)，(b)图中，右下角的矩形中的各点都+1了，可以试着结合一维差分的证明理解一下wsm。(c)，(d)图其实就是相同的操作罢了。

AC代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=1e3+10;
int mat[MAXN][MAXN];
int main(){
    int n,m;cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        //上面提到的操作
        mat[x1][y1]++;
        mat[x2+1][y1]--;
        mat[x1][y2+1]--;
        mat[x2+1][y2+1]++;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            //求前缀和，处理出每个点的值
            mat[i][j]+=mat[i-1][j]+mat[i][j-1]-mat[i-1][j-1];
            cout<<mat[i][j]<<" ";
        }
        cout<<"\n";
    }
    return 0;
}

火烧赤壁

题目背景

曹操平定北方以后，公元 208 年，率领大军南下，进攻刘表。他的人马还没有到荆州，刘表已经病死。他的儿子刘琮听到曹军声势浩大，吓破了胆，先派人求降了。

孙权任命周瑜为都督，拨给他三万水军，叫他同刘备协力抵抗曹操。

隆冬的十一月，天气突然回暖，刮起了东南风。

没想到东吴船队离开北岸大约二里距离，前面十条大船突然同时起火。火借风势，风助火威。十条火船，好比十条火龙一样，闯进曹军水寨。那里的船舰，都挤在一起，又躲不开，很快地都烧起来。一眨眼工夫，已经烧成一片火海。

曹操气急败坏的把你找来，要你钻入火海把连环线上着火的船只的长度统计出来！

题目描述

给定每个起火部分的起点和终点，请你求出燃烧位置的长度之和。

输入格式

第一行一个整数，表示起火的信息条数 \(n\)。
接下来 \(n\) 行，每行两个整数 \(a, b\)，表示一个着火位置的起点和终点（注意：左闭右开）。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

3
-1 1
5 11
2 9

样例输出 #1

11

提示

数据规模与约定

对于全部的测试点，保证 \(1 \leq n \leq 2 \times 10^4\)，\(-2^{31} \leq a \leq b \lt 2^{31}\)，且答案小于 \(2^{31}\)。 ## 思路分析 实际上这是一道离散化的题目，但是我当初做的时候还不会离散化qwq，看了题解区大佬的绝妙思路： 大佬的题解 可以发现，覆盖的范围是一样的，那么我们可以这样操作： 1、将起点和终点排个序。 2、将他们按照从小到大的顺序一一匹配，计算长度。 3、如果有重复的覆盖范围，减去即可。（也就是当前的终点坐标比下一个的起点坐标大时） ## AC代码

#include<iostream>
#include<algorithm>
using namespace std;
using ll = long long;
int n;
ll a[20200], b[20200], l;
int main() {
	cin >> n; 
	for (int i = 1; i <= n; i++) {
		cin >> a[i] >> b[i];
	}
	sort(a + 1, a + 1 + n);
	sort(b + 1, b + 1 + n);
	for (int i = 1; i <= n; i++) {
		l += b[i] - a[i];
		//注意i<n,因为a[n]，b[n]是最后的起点和终点
		if (i < n) {
			if (b[i] > a[i + 1]) {
				l -= b[i] - a[i + 1];
			}
		}
	}
	cout << l;
	return 0;
}

领地选择

题目描述

作为在虚拟世界里统帅千军万马的领袖，小 Z 认为天时、地利、人和三者是缺一不可的，所以，谨慎地选择首都的位置对于小 Z 来说是非常重要的。

首都被认为是一个占地 \(C\times C\) 的正方形。小 Z 希望你寻找到一个合适的位置，使得首都所占领的位置的土地价值和最高。

输入格式

第一行三个整数 \(N,M,C\)，表示地图的宽和长以及首都的边长。

接下来 \(N\) 行每行 \(M\) 个整数，表示了地图上每个地块的价值。价值可能为负数。

输出格式

一行两个整数 \(X,Y\)，表示首都左上角的坐标。

样例 #1

样例输入 #1

3 4 2
1 2 3 1
-1 9 0 2
2 0 1 1

样例输出 #1

1 2

提示

对于 \(60\%\) 的数据，\(N,M\le 50\)。

对于 \(90\%\) 的数据，\(N,M\le 300\)。

对于 \(100\%\) 的数据，\(1\le N,M\le 10^3\)，\(1\le C\le \min(N,M)\)。 ## 思路分析 二维前缀和的练习题，不解释了qwq。 ## AC代码

#include<iostream>
using namespace std;
using ll = long long;
ll n, m, c;
ll map[1010][1010], sum[1010][1010], maxn = -999999999, nx,ny;
int main() {
	cin >> n >> m >> c;
	for (ll i = 1; i <= n; i++) {
		for (ll j = 1; j <= m; j++) {
			cin >> map[i][j];
			//求前缀和
			sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + map[i][j];
		}
	}
	for (int i = c; i <= n; i++) {
		for (int j = c; j <= m; j++) {
		    //枚举以(i,j)为右下角、边长为c的正方形的面积，注意更新坐标
			if (sum[i][j] - sum[i - c][j] - sum[i][j - c] + sum[i - c][j - c] > maxn) {
				maxn = sum[i][j] - sum[i - c][j] - sum[i][j - c] + sum[i - c][j - c];
				nx = i - c + 1;
				ny = j - c + 1;
			}
		}
	}
	cout << nx << " " << ny;
	return 0;
}

聪明的质检员

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 \(n\) 个矿石，从 \(1\) 到 \(n\) 逐一编号，每个矿石都有自己的重量 \(w_i\) 以及价值 \(v_i\) 。检验矿产的流程是：

1. 给定$ m$ 个区间 \([l_i,r_i]\)；
2. 选出一个参数 \(W\)；
3. 对于一个区间 \([l_i,r_i]\)，计算矿石在这个区间上的检验值 \(y_i\)：

\[y_i=\sum\limits_{j=l_i}^{r_i}[w_j \ge W] \times \sum\limits_{j=l_i}^{r_i}[w_j \ge W]v_j\]

其中 \(j\) 为矿石编号。

这批矿产的检验结果 \(y\) 为各个区间的检验值之和。即：\(\sum\limits_{i=1}^m y_i\)

若这批矿产的检验结果与所给标准值 \(s\) 相差太多，就需要再去检验另一批矿产。小T 不想费时间去检验另一批矿产，所以他想通过调整参数 \(W\) 的值，让检验结果尽可能的靠近标准值 \(s\)，即使得 \(|s-y|\) 最小。请你帮忙求出这个最小值。

输入格式

第一行包含三个整数 \(n,m,s\)，分别表示矿石的个数、区间的个数和标准值。

接下来的 \(n\) 行，每行两个整数，中间用空格隔开，第 \(i+1\) 行表示 \(i\) 号矿石的重量 \(w_i\) 和价值 \(v_i\)。

接下来的 \(m\) 行，表示区间，每行两个整数，中间用空格隔开，第 \(i+n+1\) 行表示区间 \([l_i,r_i]\) 的两个端点 \(l_i\) 和 \(r_i\)。注意：不同区间可能重合或相互重叠。

输出格式

一个整数，表示所求的最小值。

样例 #1

样例输入 #1

5 3 15 1 5 2 5 3 5 4 5 5 5 1 5 2 4 3 3

样例输出 #1

10

提示

【输入输出样例说明】

当 \(W\) 选 \(4\) 的时候，三个区间上检验值分别为 \(20,5 ,0\) ，这批矿产的检验结果为 \(25\)，此时与标准值 \(S\) 相差最小为 \(10\)。

【数据范围】

对于 \(10\%\) 的数据，有 \(1 ≤n ,m≤10\)；

对于 \(30\%\)的数据，有 \(1 ≤n ,m≤500\) ；

对于 \(50\%\) 的数据，有 \(1 ≤n ,m≤5,000\)； 对于 \(70\%\) 的数据，有 \(1 ≤n ,m≤10,000\) ；

对于 \(100\%\) 的数据，有 \(1 ≤n ,m≤200,000\)，\(0 < w_i,v_i≤10^6\)，\(0 < s≤10^{12}\)，\(1 ≤l_i ≤r_i ≤n\) ## 思路分析 直接暴力枚举求出这个点肯定不行，并且看到题目要求最小值，所以可以猜测：使用二分。 二分的是\(W\)的值，\(check(mid)\)的判断条件是\(s-\sum\limits_{i=1}^m y_i\)是否大于0，由此缩减二分的范围，分析一下单调性：当\(W\)减少时，\(\sum\limits_{i=1}^m y_i\)增大，反之，则变小，并且当\(W\)足够小时，\(\sum\limits_{i=1}^m y_i\)会大于\(s\),符合单调性，可以使用二分。具体看看注释。 还需要先预处理出前缀和：包括个数和总价值，否则会TLE。 ## AC代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=2e5+10;
int v[MAXN],w[MAXN],l[MAXN],r[MAXN],cnt_num[MAXN],cnt_val[MAXN];
int main(){
    int n,m;
    ll sum,ans,s;
    cin>>n>>m>>s;
    ans=s;
    for(int i=1;i<=n;i++){
        //w是矿石的重量，v是矿石的价值
        cin>>w[i]>>v[i];
    }
    for(int i=1;i<=m;i++){
        //输入的是查询的区间
        cin>>l[i]>>r[i];
    }
    int left=0,right=2e6+10;
    while(left<right){
        int mid=(left+right)>>1;
        sum=0;
        memset(cnt_num,0,sizeof(cnt_num));
        memset(cnt_val,0,sizeof(cnt_val));
        //利用前缀和，预处理出合格品的个数和总价值
        for(int i =1;i<=n;i++){
            if(w[i]>=mid){
                cnt_num[i]=cnt_num[i-1]+1;
                cnt_val[i]=cnt_val[i-1]+v[i];
            }
            else{
                cnt_num[i]=cnt_num[i-1];
                cnt_val[i]=cnt_val[i-1];
            }
        }
        //统计一下检测结果，也就是查询的各个区间总价值之和
        for(int i=1;i<=m;i++){
            sum+=(cnt_val[r[i]]-cnt_val[l[i]-1])*(cnt_num[r[i]]-cnt_num[l[i]-1]);
        }
        //注意更新答案，得到的是最小值，注意ans初始化为无穷大
        ans=min(ans,abs(sum-s));
        //说明这个解合法，将右端点确定下来
        if(sum<=s)right=mid;
        //否则，将左端点确定下来
        else left=mid+1;
    }
    cout<<ans<<"\n";
    return 0;
}

程序自动分析

[NOI2015] 程序自动分析

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 \(x_1,x_2,x_3,\cdots\) 代表程序中出现的变量，给定 \(n\) 个形如 \(x_i=x_j\) 或 \(x_i\neq x_j\) 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：\(x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1\)，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

输入的第一行包含一个正整数 \(t\)，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 \(n\)，表示该问题中需要被满足的约束条件个数。接下来 \(n\) 行，每行包括三个整数 \(i,j,e\)，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 \(e=1\)，则该约束条件为 \(x_i=x_j\)。若\(e=0\)，则该约束条件为 \(x_i\neq x_j\)。

输出格式

输出包括 \(t\) 行。

输出文件的第 \(k\) 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 \(k\) 个问题判定为可以被满足，NO 表示不可被满足。

样例 #1

样例输入 #1

2 2 1 2 1 1 2 0 2 1 2 1 2 1 1

样例输出 #1

NO YES

样例 #2

样例输入 #2

2 3 1 2 1 2 3 1 3 1 1 4 1 2 1 2 3 1 3 4 1 1 4 0

样例输出 #2

YES NO

提示

【样例解释1】

在第一个问题中，约束条件为：\(x_1=x_2,x_1\neq x_2\)。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：\(x_1=x_2,x_1 = x_2\)。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：\(x_1=x_2,x_2= x_3,x_3=x_1\)。只需赋值使得 \(x_1=x_2=x_3\)，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：\(x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1\)。由前三个约束条件可以推出 \(x_1=x_2=x_3=x_4\)，然而最后一个约束条件却要求 \(x_1\neq x_4\)，因此不可被满足。

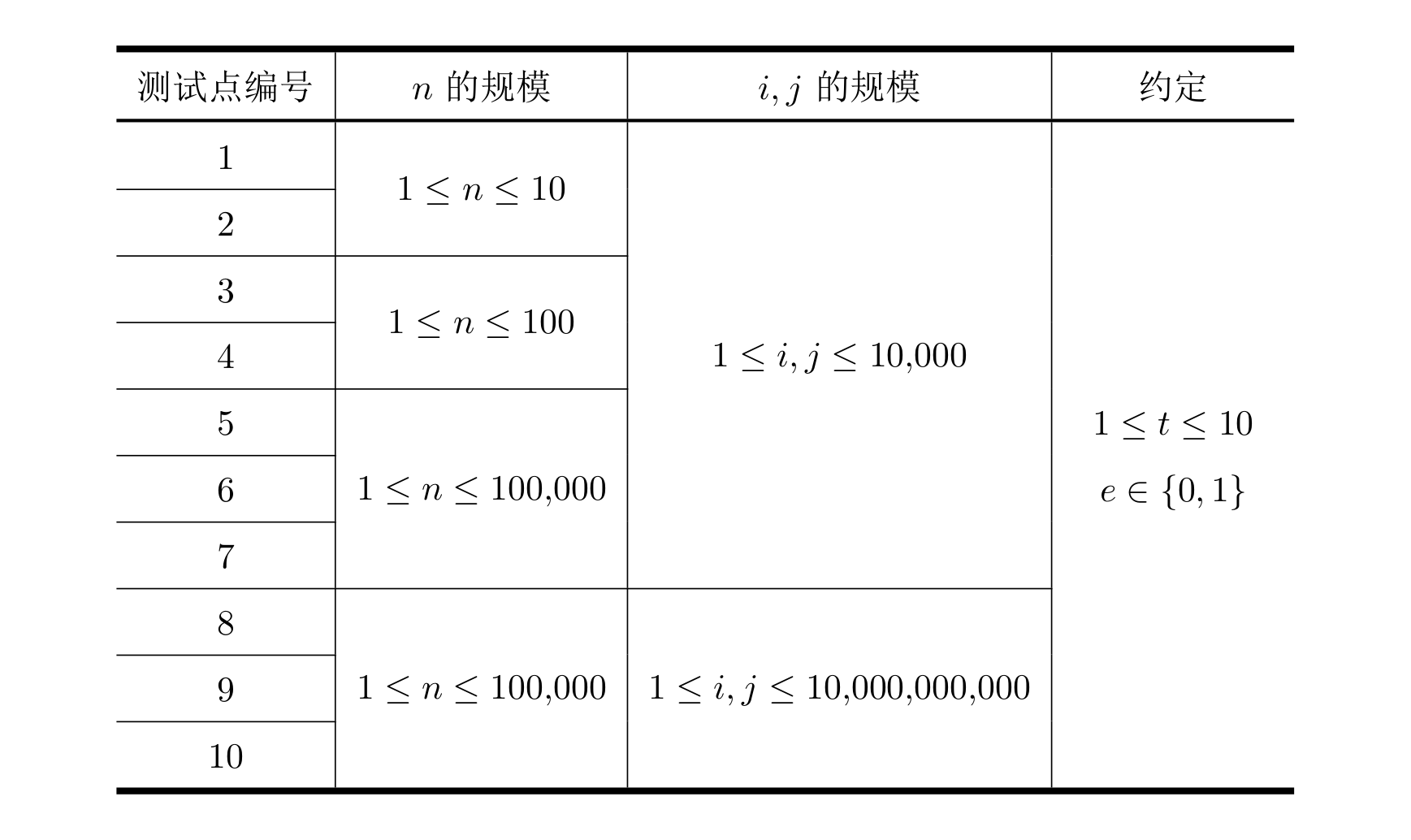
【数据范围】

所有测试数据的范围和特点如下表所示：

勘误：测试点 \(8 \sim 10\) 的 \(i, j\) 约束为 \(1 \leq i, j \leq 10^9\)，而不是下图中的 \(10^{10}\)。

## 思路分析 这个其实是并查集+离散化，但是离散化我还不太熟，暂时没写。当初用了\(unordered-map\)混过去了qwq。 说正题，这道题有两个特征，查询和赋值，我们分析一下，这其实跟并查集的功能很相似，并查集维护的是一些元素的分组，用的是查询和合并两个操作。这里的赋值，我们其实可以用合并来实现： 1、如果是赋值，合并为一组。 2、如果是查询，那么我们只要看两者是否在同一组内即可。 这里并查集写的是按秩合并，不会的可以用普通的并查集代替。 ## AC代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+10;
unordered_map<int,int>pre;
unordered_map<int,int>Rank;
int x[MAXN],y[MAXN],e[MAXN];
//并查集的查询功能
int find(int x){
    if(x==pre[x])return x;
    return pre[x]=find(pre[x]);
}
//并查集的合并功能
void join(int x,int y){
    int fx=find(x),fy=find(y);
    if(Rank[fx]>=Rank[fy])pre[fy]=fx;
    else pre[fx]=fy;
    if(Rank[fx]==Rank[fy]&&fx!=fy)Rank[fx]++;
}
void solve(){
    //注意清空数组，因为有多组数据输入，不然喜迎WA qwq
    pre.clear();
    Rank.clear();
    memset(x,0,sizeof(x));
    memset(y,0,sizeof(y));
    memset(e,0,sizeof(e));
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        //输入元素，以及对应的操作，注意在原题中指的是下标x，y
        cin>>x[i]>>y[i]>>e[i];
        //将并查集初始化
        pre[x[i]]=x[i];
        pre[y[i]]=y[i];
        //按秩合并才需要的初始化，其实这一行也可以不用写@~@
        Rank[x[i]]=1,Rank[y[i]]=1;
    }
    for(int i=1;i<=n;i++){
        //如果是1，合并两个元素
        if(e[i])join(x[i],y[i]);
    }
    for(int i=1;i<=n;i++){
        //如果不是1，查看两者的祖先是否一样
        if(!e[i]){
            //不一样的话，直接输出NO，return 0
            if(find(x[i])==find(y[i])){
                cout<<"NO\n";
                return;
            }
        }
    }
    //经历重重困难，终于是YES了！！！
    cout<<"YES\n";
}
int main(){
    int t;
    cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

[USACO11MAR] Brownie Slicing G

题面翻译

Bessie烘焙了一块巧克力蛋糕。这块蛋糕是由 \(R\times C(1\leq R,C\leq 500)\) 个小的巧克力蛋糕组成的。第 \(i\) 行，第 \(j\) 列的蛋糕有 \(N_{i,j}(N_{i,j}\leq 4000)\) 块巧克力碎屑。

Bessie想把蛋糕分成 \(A\times B(1\leq A\leq R,1\leq B\leq C)\) 块，:给 \(A\times B\) 只奶牛。蛋糕先水平地切 \(A-1\) 刀（只能切沿整数坐标切）来把蛋糕划分成 \(A\) 块。然后再把剩下来的每一块独立地切 \(B-1\) 刀，也只能切沿整数坐标切。其他 \(A\times B-1\) 只奶牛就每人选一块，留下一块给Bessie。由于贪心，他们只会留给Bessie巧克力碎屑最少的那块。求出Bessie最优情况下会获得多少巧克力碎屑。

例如，考虑一个\(5\times4\)的蛋糕，上面的碎屑分布如下图所示：

1 2 2 1
3 1 1 1
2 0 1 3
1 1 1 1
1 1 1 1

Bessie必须把蛋糕切成4条，每条分成2块。Bessie能像这样切蛋糕:

1 2 | 2 1
---------
3 | 1 1 1
---------
2 0 1 | 3
---------
1 1 | 1 1
1 1 | 1 1

这样，Bessie至少能获得 \(3\) 块巧克力碎屑

题目描述

Bessie has baked a rectangular brownie that can be thought of as an RxC grid (1 <= R <= 500; 1 <= C <= 500) of little brownie squares. The square at row i, column j contains N_ij (0 <= N_ij <= 4,000) chocolate chips.

Bessie wants to partition the brownie up into A*B chunks (1 <= A <= R; 1 <= B <= C): one for each of the A*B cows. The brownie is cut by first making A-1 horizontal cuts (always along integer

coordinates) to divide the brownie into A strips. Then cut each strip *independently* with B-1 vertical cuts, also on integer

boundaries. The other A*B-1 cows then each choose a brownie piece, leaving the last chunk for Bessie. Being greedy, they leave Bessie the brownie that has the least number of chocolate chips on it.

Determine the maximum number of chocolate chips Bessie can receive, assuming she cuts the brownies optimally.

As an example, consider a 5 row x 4 column brownie with chips

distributed like this:

1 2 2 1
3 1 1 1
2 0 1 3
1 1 1 1
1 1 1 1

Bessie must partition the brownie into 4 horizontal strips, each with two pieces. Bessie can cut the brownie like this:

1 2 | 2 1
---------
3 | 1 1 1
---------
2 0 1 | 3
---------
1 1 | 1 1
1 1 | 1 1

Thus, when the other greedy cows take their brownie piece, Bessie still gets 3 chocolate chips.

Bessie烘焙了一块巧克力蛋糕。这块蛋糕是由R*C(1 <= R,C <= 500)个小的巧克力蛋糕组成的。第i行，第j列的蛋糕有N_ij(1<= N_ij <= 4,000)块巧克力碎屑。

Bessie想把蛋糕分成A*B块，(1 <= A<= R,1 <= B <= C): 给A*B只奶牛。蛋糕先水平地切A-1刀（只能切沿整数坐标切）来把蛋糕划分成A块。然后再把剩下来的每一块独立地切B-1刀，也只能切沿整数坐标切。其他A*B-1只奶牛就每人选一块，留下一块给Bessie。由于贪心，他们只会留给Bessie巧克力碎屑最少的那块。求出Bessie最优情况下会获得多少巧克力碎屑。

例如，考虑一个5*4的蛋糕，上面的碎屑分布如下图所示：

1 2 2 1
3 1 1 1
2 0 1 3
1 1 1 1
1 1 1 1

Bessie必须把蛋糕切成4条，每条分成2块。Bessie能像这样切蛋糕:

输入格式

* Line 1: Four space-separated integers: R, C, A, and B

* Lines 2..R+1: Line i+1 contains C space-separated integers: N_i1, ..., N_iC

输出格式

* Line 1: A single integer: the maximum number of chocolate chips that Bessie guarantee on her brownie

样例 #1

样例输入 #1

5 4 4 2 
1 2 2 1 
3 1 1 1 
2 0 1 3 
1 1 1 1 
1 1 1 1

样例输出 #1

3

思路分析

当初也没想出来怎么二分，看了题解区大佬的题解恍然大悟。 蛋糕要分成\(A * B\)块，注意可以先分成\(A\)横块，每一块再分成\(B\)条，也就是切条时可以不用一刀切！！！ 那么要统计一块蛋糕的巧克力屑，肯定就是使用前缀和了。我们也可以先预处理出前缀和，再进行二分。 二分的是巧克力屑的数量，\(check(mid)\)的是能否切出\(A*B\)块蛋糕，具体\(check(mid)\)怎么写可以看看代码+注释。 ## AC代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=2e6+10;
int cake[510][510],line[510][510],pre[510][510],r,c,a,b,ans;
bool check(int x){
    int num=0,last=0;
    //我们先切一行，再将这一行切成B列，看看最终能否满足A*B块蛋糕
    for(int i=1;i<=r;i++){
        int cnt=0,sum_cake=0;
        //i枚举的是当前行，j枚举的是当前列，last记录的是上一块（行）蛋糕的最底行
        for(int j=1;j<=c;j++){
            //判断当前切的蛋糕的巧克力屑的数量是否大于x，也就是二分的值
            //我们一列一列的补充蛋糕，判断补充后，其巧克力屑数目是否大于x，不满足，则补充。
            if(sum_cake+(pre[i][j]-pre[i][j-1])-(pre[last][j]-pre[last][j-1])<x){
                sum_cake+=(pre[i][j]-pre[i][j-1])-(pre[last][j]-pre[last][j-1]);
            }
            //满足，另开一列，注意统计的蛋糕数目+1，蛋糕上的巧克力屑数目重置为0
            else{
                sum_cake=0;
                cnt++;
            }
        }
        //判断这一行蛋糕，切出来是否有B块
        if(cnt>=b){
        //如果有B块，我们则记录这块蛋糕的最后一行，并且记录 行的蛋糕数量++，没有只能再加上一行继续切了，直到满足为止。
            last=i;
            num++;
        }
    }
    //看看是否能不能切除A行蛋糕，满足return true，否则，返回false
    if(num<a)return false;
    else return true;
}
int main(){
    ios::sync_with_stdio(0);
    //输入R、C、A、B
    cin>>r>>c>>a>>b;
    //输入蛋糕的巧克力屑
    for(int i=1;i<=r;i++){
        for(int j=1;j<=c;j++){
            cin>>cake[i][j];
        }
    }
    //预处理出前缀和
    for(int i=1;i<=r;i++){
        for(int j=1;j<=c;j++){
            pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+cake[i][j];
        }
    }
    int left=0,right=MAXN;
    //二分，不多说了，重点在check(x)
    while(left<=right){
        int mid=(left+right)>>1;
        if(check(mid)){
            ans=mid;
            left=mid+1;
        }
        else{
            right=mid-1;
        }
    }
    cout<<ans<<"\n";
}

海底高铁

思路分析

先想想暴力怎么办？我们可以先统计每段铁路要经过几次，再贪心，看看是办卡优惠还是买票优惠。 但是这样肯定会TLE，想想怎么改——————前缀和吗？不对，前缀和求的是多个元素之间的关系。 差分吗？差分维护的是多个元素之间的逻辑关系，最终得到的是单个元素。 那就是差分了！我们可以利用它来得出每段铁路经过的次数，想想差分的作用，O(1)修改区间的值，O(n)查询单个元素的值。基于此，我们可以先O(1)预处理区间总共要修改的值，再O(n)得到每段铁路经过的次数，最后贪心得出最小花费。具体可以看看注释。 可以看看这篇搞笑的故事，相信会有所收获。 ## AC代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=1e5+10;
ll p[MAXN],a[MAXN],b[MAXN],c[MAXN],ans[MAXN];
int main(){
    int n,m;cin>>n>>m;
    ll sum=0;
    for(int i=1;i<=m;i++)cin>>p[i];
    for(int i=1;i<n;i++){
        cin>>a[i]>>b[i]>>c[i];
    }
    //利用差分，统计修改次数，注意相邻元素不一定是从小到大，所以可能得交换顺序
    //一般来说，是d[l]++,d[r+1]--。l指的是左端点，r指的是右端点，但是我们这里d[l]++,d[r]--即可，因为其实从r城市出发的铁路我们根本不需要经过。
    for(int i=1;i<m;i++){
        ans[min(p[i],p[i+1])]++;
        ans[max(p[i],p[i+1])]--;
    }
    //利用差分得出每段铁路需要经过的次数
    for(int i=1;i<=n;i++){
        ans[i]+=ans[i-1];
    }
    //贪心，看看每一段铁路是买票优惠还是买卡优惠
    for(int i=1;i<n;i++){
        sum+=min(ans[i]*a[i],ans[i]*b[i]+c[i]);
    }
    cout<<sum<<"\n";
    return 0;
}

[Poetize6] IncDec Sequence

[Poetize6] IncDec Sequence

题目描述

给定一个长度为 \(n\) 的数列 \({a_1,a_2,\cdots,a_n}\)，每次可以选择一个区间\([l,r]\)，使这个区间内的数都加 \(1\) 或者都减 \(1\)。 请问至少需要多少次操作才能使数列中的所有数都一样，并求出在保证最少次数的前提下，最终得到的数列有多少种。

输入格式

第一行一个正整数 \(n\) 接下来 \(n\) 行,每行一个整数,第 $i+1 $行的整数表示 \(a_i\)。

输出格式

第一行输出最少操作次数 第二行输出最终能得到多少种结果

样例 #1

样例输入 #1

4 1 1 2 2

样例输出 #1

1 2

提示

对于 \(100\%\) 的数据，\(n\le 100000, 0 \le a_i \le 2^{31}\)。 ## 思路分析 先想想元素相同？其实就是他们的差都是0，我们关注的是单个元素，并且是各元素之间的逻辑关系问题，所以我们使用差分来求解。 那么问题就变成了怎么让差分数组全为0（除了\(diff[1]\)不为0，因为\(a[0]\)为0），对一个区间\([l,r]\)进行修改，其实就是\(diff[l]++\)、\(dff[r+1]--\)。而一个差分数组里元素肯定有正有负，最好的情况是，一次修改，可以让一个负数加1，一个正数减1，这样操作步骤就是最少的。 但是如果只剩下正数或者负数，就只能一次一次进行了。 至于有多少可能结果，其实就是最后只剩正数或者负数时，一步步修改的操作次数了。为什么？ 前面修改的时候，我们修改的是\([l,r]\)，对\(diff[1]\)无影响，而只剩正数或者负数时，我们可以\(diff[1]++\)\(diff[x]--\)了，也可以\(diff[1]--\)\(diff[x]++\)，也可以不动，所以可能的结果就是：剩余的正数/负数+1，因为本身不修改，也要加上。 ## AC代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=1e5+10;
ll a[MAXN];
int main(){
    ll n,x=0,y=0,d;cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=2;i<=n;i++){
        //求差分数组：x统计正数，y统计负数
        d=a[i]-a[i-1];
        if(d>0)x+=d;
        else y-=d;
    }
    //严格的证明是:ans1=min(x,y)+abs(x-y),所以ans1=max(x,y)。
    ll ans1=max(x,y);
    //不解释了，看看上面
    ll ans2=abs(x-y)+1;
    cout<<ans1<<"\n"<<ans2;
    return 0;
}

[NOIP2012 提高组] 借教室

题目描述

在大学期间，经常需要租借教室。大到院系举办活动，小到学习小组自习讨论，都需要向学校申请借教室。教室的大小功能不同，借教室人的身份不同，借教室的手续也不一样。

面对海量租借教室的信息，我们自然希望编程解决这个问题。

我们需要处理接下来 \(n\) 天的借教室信息，其中第 \(i\) 天学校有 \(r_i\) 个教室可供租借。共有 \(m\) 份订单，每份订单用三个正整数描述，分别为 \(d_j,s_j,t_j\)，表示某租借者需要从第 \(s_j\) 天到第 \(t_j\) 天租借教室（包括第 \(s_j\) 天和第 \(t_j\) 天），每天需要租借 \(d_j\) 个教室。

我们假定，租借者对教室的大小、地点没有要求。即对于每份订单，我们只需要每天提供 \(d_j\) 个教室，而它们具体是哪些教室，每天是否是相同的教室则不用考虑。

借教室的原则是先到先得，也就是说我们要按照订单的先后顺序依次为每份订单分配教室。如果在分配的过程中遇到一份订单无法完全满足，则需要停止教室的分配，通知当前申请人修改订单。这里的无法满足指从第 \(s_j\) 天到第 \(t_j\) 天中有至少一天剩余的教室数量不足 \(d_j\) 个。

现在我们需要知道，是否会有订单无法完全满足。如果有，需要通知哪一个申请人修改订单。

输入格式

第一行包含两个正整数 \(n,m\)，表示天数和订单的数量。

第二行包含 \(n\) 个正整数，其中第 \(i\) 个数为 \(r_i\)，表示第 \(i\) 天可用于租借的教室数量。

接下来有 \(m\) 行，每行包含三个正整数 \(d_j,s_j,t_j\)，表示租借的数量，租借开始、结束分别在第几天。

每行相邻的两个数之间均用一个空格隔开。天数与订单均用从 \(1\) 开始的整数编号。

输出格式

如果所有订单均可满足，则输出只有一行，包含一个整数 \(0\)。否则（订单无法完全满足）

输出两行，第一行输出一个负整数 \(-1\)，第二行输出需要修改订单的申请人编号。

样例 #1

样例输入 #1

4 3 
2 5 4 3 
2 1 3 
3 2 4 
4 2 4

样例输出 #1

-1 
2

提示

【输入输出样例说明】

第 \(1\)份订单满足后，\(4\)天剩余的教室数分别为 \(0,3,2,3\)。第 \(2\) 份订单要求第 \(2\)天到第 \(4\) 天每天提供\(3\)个教室，而第 \(3\) 天剩余的教室数为\(2\)，因此无法满足。分配停止，通知第\(2\) 个申请人修改订单。

【数据范围】

对于10%的数据，有\(1≤ n,m≤ 10\)；

对于30%的数据，有\(1≤ n,m≤1000\)；

对于 70%的数据，有\(1 ≤ n,m ≤ 10^5\)；

对于 100%的数据，有\(1 ≤ n,m ≤ 10^6,0 ≤ r_i,d_j≤ 10^9,1 ≤ s_j≤ t_j≤ n\)。

NOIP 2012 提高组 第二天 第二题

2022.2.20 新增一组 hack 数据 ## 思路分析 （这道当初也不会qwq，看了题解大佬——皎月半洒花的博客）还是想想暴力，可以暴力先枚举订单数量，然后减少可以使用的教室数目，直到超过上限为止，但是这肯定会TLE。 想想怎么办？我们修改的是教室的数目，并且是一个区间，所以想到的是差分。 因为需要找到哪一个不满足，所以加上二分进行查询即可。 引用大佬的话：

一般来说，二分是个很有用的优化途径，因为这样会直接导致减半运算，而对于能否二分，有一个界定标准：状态的决策过程或者序列是否满足单调性或者可以局部舍弃性。 而在这个题里，因为如果前一份订单都不满足，那么之后的所有订单都不用继续考虑；而如果后一份订单都满足，那么之前的所有订单一定都可以满足，符合局部舍弃性，所以可以二分订单数量。

AC代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=1e6+10;
ll r[MAXN],d_j[MAXN],s_j[MAXN],t_j[MAXN],diff[MAXN],need[MAXN],ans,n,m;
bool check(int x){
    memset(diff,0,sizeof(diff));
    //利用差分进行区间修改
    for(int i=1;i<=x;i++){
        diff[s_j[i]]+=d_j[i];
        diff[t_j[i]+1]-=d_j[i];
    }
    //利用差分得到每天需要的教室数目
    for(int i=1;i<=n;i++){
        need[i]=need[i-1]+diff[i];
        //看看每天的教室数目能否满足需求
        if(need[i]>r[i])return 0;
    }
    return 1;
}
int main(){
    ios::sync_with_stdio(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>r[i];
    }
    for(int i=1;i<=m;i++){
        cin>>d_j[i]>>s_j[i]>>t_j[i];
    }
    //可以先判断是否能全部满足，如果能输出0
    if(check(m)){
        cout<<0;
        return 0;
    }
    int left=1,right=m;
    //二分的是订单号，check的是每天的教室数目能否满足
    while(left<right){
        int mid=(left+right)/2;
        if(check(mid)){
            left=mid+1;
        }
        else{
            right=mid;
        }
    }
    cout<<-1<<"\n"<<left;
}