莫尔效应及光栅传感实验

【实验目的】

理解莫尔现象的产生机理
观察直线光栅、径向圆光栅、切向圆光栅的莫尔条纹并验证其特性
用直线光栅及圆光栅测量线位移

【实验原理】

两只光栅以很小的交角相向叠合时,在相干或非相干光的照明下，在叠合面上将出现明暗相间的条纹，称为莫尔条纹。莫尔条纹现象是光栅传感器的理论基础，它可以用粗光栅或细光栅形成。栅距远大于波长的光栅叫粗光栅，栅距接近波长的光栅叫细光栅。

1.直线光栅莫尔条纹

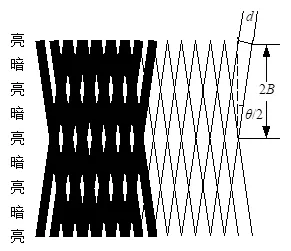
两只光栅常数相同的光栅，其刻划面相向叠合并且使两者栅线有很小的交角\(θ\)，则由于挡光效应（光栅常数\(d\) >20μm）或光的衍射作用（光栅常数\(d\) <10μm），在与光栅刻线大致垂直的方向上形成明暗相间的条纹，如图1（左）所示。

设主光栅与副光栅之间的夹角为\(θ\)，莫尔条纹间距为\(B\)：

可得： \[ B=\frac{d}{2sin\frac{θ}{2}} \]

式中\(θ\)的单位为弧度。由上式可知，当改变光栅夹角\(θ\)，莫尔条纹宽度\(B\)也将随之改变。

对于直线光栅的莫尔条纹有如下主要特性：

（1）在保持两光栅交角一定的情况下，使一个光栅固定，另一个光栅沿栅线的垂直方向运动，每移动一个栅距\(d\)，莫尔条纹移动一个条纹间距\(B\)，若光栅反向运动，则莫尔条纹的移动方向也相反。

（2）当两光栅交角\(θ\)很小时，相当于把栅距\(d\)放大了1/\(θ\)倍，莫尔条纹可以将很小的光栅位移同步放大为莫尔条纹的位移。

（3）测得莫尔条纹移动的个数\(k\)就可以得到光栅的位移Δ\(L\)为Δ\(L\)=\(kd\)。

（4）光电器件获取的莫尔条纹是两光栅重合区域所有光栅线综合作用的结果。即使光栅在刻画过程中有误差，莫尔条纹对刻画误差有平均作用，从而在很大程度上消除栅距的局部误差的影响，这是光栅传感器精度高的重要原因。

2.径向圆光栅莫尔条纹

径向圆光栅是指大量在空间均匀分布且指向圆心的刻线形成的光栅，相邻刻线之间的夹角\(α\)称为栅距角。图 2a是径向圆光栅，图 2b是两只栅距角相同（即\(α_1\)=\(α_2\)=\(α\)），圆心相距\(2S\)的径向圆光栅相向叠合产生的莫尔条纹。

图 b 径向圆光栅及径向圆光栅莫尔条纹

两只栅距角\(α\)相同的径向圆光栅组成光栅传感器。对于径向圆光栅的莫尔条纹，当其中一只光栅转动时，圆族将向外扩张或向内收缩。每转动1个栅距角，莫尔条纹移动一个条纹宽度。用光电器件测得莫尔条纹移动的个数k就可以得到光栅的角位移\(Δθ=kα\)。用径向圆光栅测量角位移具有误差减小作用。莫尔条纹是由上下\(2\)组不同半径，不同圆心的圆族组成。\(k\)越大，莫尔条纹半径越小，条纹间距也越小，所以靠近传感器中心的莫尔条纹不易分辨，半径最小值为\(S\)。

3.切向圆光栅莫尔条纹

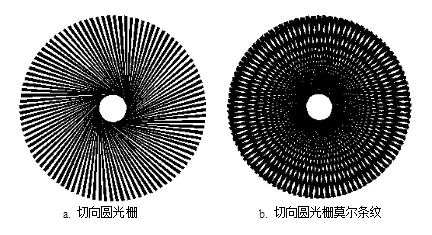
切向圆光栅是由空间分布均匀且都与一个半径很小的圆相切的众多刻线构成的圆光栅。当如图 3a的两只切向圆光栅相向叠合时，两只光栅的切线方向相反。图 3b是两只小圆半径相同，栅距角相同的切向圆光栅相向叠合产生的莫尔条纹。

图 3 切向圆光栅与切向圆光栅莫尔条纹

设两块切向圆光栅，栅距角\(α\)相同，栅线分别切于半径为\(r_1\)与\(r_2\)的两个小圆上，两光栅切线方向相反。

对于切向圆光栅的莫尔条纹，当其中一只光栅转动时，圆族将向外扩张或向内收缩。每转动1个栅距角，莫尔条纹移动一个条纹宽度。用光电器件测得莫尔条纹移动的个数\(k\)就可以得到光栅的角位移Δ\(θ\)=\(kα\)，用切向圆光栅测量角位移具有误差减小作用。莫尔条纹是一组同心圆环，圆环半径为\(R=\frac{2r}{kα}\)，相邻圆环的间隔为\(ΔR=\frac{2r}{2kα}\)。\(k\)越大，莫尔条纹半径越小，条纹间距也越小，所以靠近传感器中心的莫尔条纹不易分辨。

【实验仪器】

仪器由主光栅基座、副光栅滑座、摄像头及监视器等组成，如图 4 所示。

图 5 实验装置结构图

主光栅基座由主光栅板和位移装置构成，主光栅板上印有原理中介绍的三种光栅。转动百分手轮，滑块会带动副光栅滑座上的副光栅与主光栅产生相应位移。副光栅滑座由副光栅、可转动副光栅座及角度读数盘组成。副光栅安装于副光栅座，转动副光栅座可改变主副光栅之间的交角，其角度由角度读数盘读出。摄像头及监视器用于观察和测量莫尔条纹特性，由摄像头升降台、摄像头及监视器组成。

【实验内容与步骤】

1.利用直线光栅测量线位移

（1）若监视器关闭，则需按一下监视器旁边的监视器开关按钮，若一切正常，监视器上将显示主光栅的放大图像。使主光栅和副光栅成一定夹角\(θ\)，使监视器上出现约3条莫尔条纹图案。

（2）转动手轮，使副光栅滑座移动到主光栅基座最右端，然后反向转动手轮使副光栅沿轨道运动，莫尔条纹随之移动。每移动5个莫尔条纹，记录副光栅的位置于表 1 中。注意：为防止回程差对实验的影响，记录副光栅位置时，百分手轮须朝同一方向进行旋转。

表 1 用直线光栅测量线位移

条纹移动数\(k\)	0	5	10	15	20
副光栅位置读数\(L_k\)(mm)	195	192	189.5	187	184.5
位移\(ΔL_k=\|L_k–L_0\|\)	0	3	5.5	8	10.5
条纹移动数\(k\)	25	30	35	40	45
副光栅位置读数\(L_k\)(mm)	182	179	177	174.5	172
位移\(ΔL_k=\|L_k–L_0\|\)	13	16	18	20.5	23

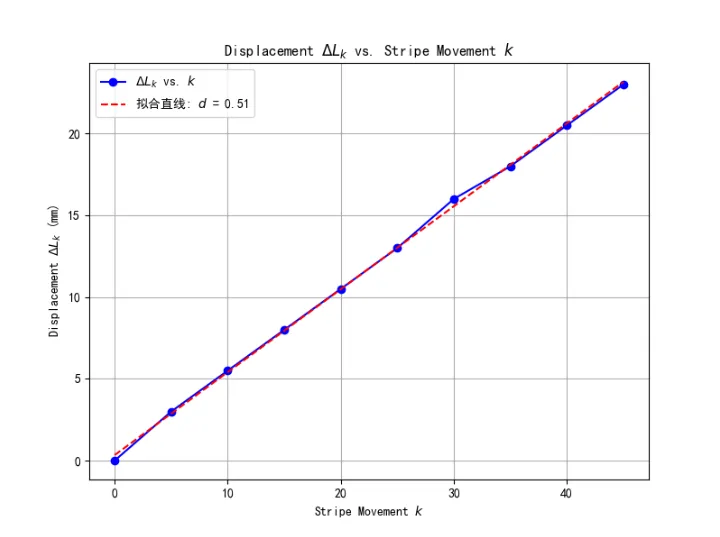
计算\(k\)为5，10，15···时对应的位移\(ΔL_k\)，填入表 1中。以\(k\)为横坐标，位移\(ΔL_k\)为纵坐标作图，可以确认曲线为直线，直线斜率\(d=0.51\)。

2.利用径向圆光栅莫尔条纹测量角位移

（1）安装摄像头，调节摄像头的位置，让摄像头监视主副光栅接近边缘的地方，直到监控器上出现清晰的莫尔条纹。

（2）沿着同一方向转动副光栅，每一栋5个莫尔条纹记录副光栅的角位置于表2中。

表 2 用径向圆光栅测量角位移

条纹移动数\(k\)	0	5	10	15	20
副光栅角位置读数\(θ_k\)(º)	0	5	10	15	19
角位移\(Δθ_k=θ_k–θ_0\)	0	5	10	15	19
条纹移动数\(k\)	25	30	35	40	45
副光栅角位置读数\(θ_k\)(º)	26	30	35	40.5	45.5
角位移\(Δθ_k=θ_k–θ_0\)	26	30	35	40.5	45.5

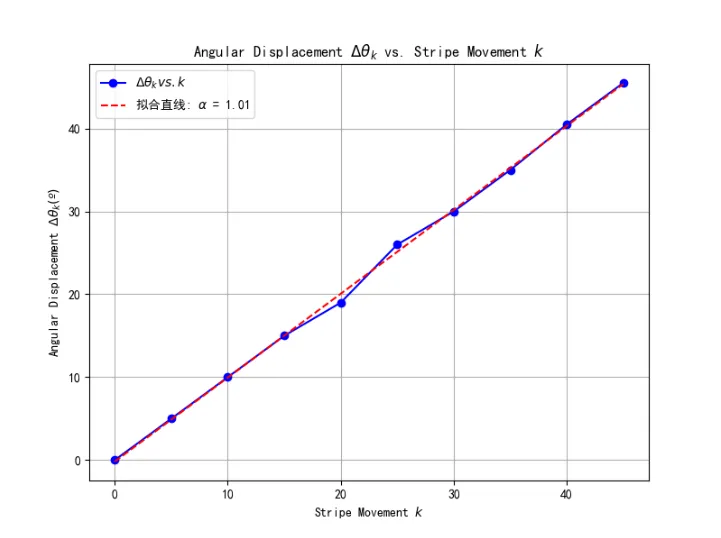
计算\(θ\)为5，10，15···时对应的角位移\(Δθ_k\)，填入表 2 中。以\(k\)为横坐标，角位移\(Δθ_k\)为纵坐标作图。可以确认曲线近似为直线，得到的拟合直线斜率\(α=1.01\)。（即验证了关系式\(Δθ=kα\)，说明可以由条纹移动数测量角位移）

已知栅距角的准确值为\(α=1.0º\)，将有直线斜率求出的栅距角值\(α\)与之比较，相对误差为： \[ \text{Relative Error} = \left| \frac{\alpha_{\text{measured}} - \alpha_{\text{true}}}{\alpha_{\text{true}}} \right| \times 100\%=\left| \frac{1.01-1.00}{1.00} \right|=0.01 \]

3.利用切向圆光栅莫尔条纹测量角位移

当监视器上出现清晰的莫尔条纹时，沿同一方向转动副光栅，每移动5个莫尔条纹记录副光栅的角位置于表 3 中。

表 3 用切向圆光栅测量角位移

条纹移动数\(k\)	0	5	10	15	20
副光栅角位置读数\(θ_k\)(º)	0	5	10	15	20
角位移\(Δθ_k=θ_k–θ_0\)	0	5º	10º	15º	20º
条纹移动数\(k\)	25	30	35	40	45
副光栅角位置读数\(θ_k\)(º)	25	30	35	40	45
角位移\(Δθ_k=θ_k–θ_0\)	25º	30º	35º	40º	45º

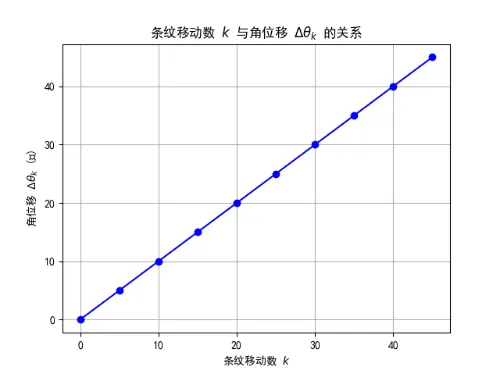
计算\(θ\)为5，10，15···时对应的角位移\(Δθ_k\)，填入表 3 中。以\(k\)为横坐标，角位移\(Δθ_k\)为纵坐标作图。可以确认曲线为直线，直线斜率\(α=1.0\)。（即验证了关系式\(Δθ=kα\)，说明可以由条纹移动数测量角位移）

已知栅距角的准确值为\(α=1.0º\)，将有直线斜率求出的栅距角值\(α\)与之比较，相对误差计算可得： \[ \text{Relative Error} = \left| \frac{\alpha_{\text{measured}} - \alpha_{\text{true}}}{\alpha_{\text{true}}} \right| \times 100\%= \left| \frac{1.00-1.00}{1.00}\right|=0.00 \]