SCUT2011 Data Structure
SCUT2011
Select the correct choice.
(5)
The linear list (
答案:(C)
答案解释:
在顺序存储的线性表(
如果要删除第一个节点,后面的
那么总的移动节点数的期望(也就是平均移动节点数)为:
所以平均移动节点数为
(6)
- Which of the following is a true statement: ( )
A general tree can be transferred to a binary tree with the root having both left child and right child.
In a BST, the node can be enumerated sorted by a preorder traversal to the BST.
In a BST, the left child of any node is less than the right child, but in a heap, the left child of any node could be less than or greater than the right child.
A heap must be full binary tree.
答案:(C)
答案解释:
选项 A: 一般树转换为二叉树采用孩子兄弟表示法,转换后的二叉树其根节点只有左子树(对应原树的第一个孩子)和右子树(对应原树第一个孩子的兄弟节点依次连接构成),并非随意根节点有左、右两个子树,所以该选项错误。
选项 B: 二叉搜索树(BST)通过中序遍历才能得到节点按关键字有序排列的序列,前序遍历并不能保证节点按排序后的顺序枚举出来,所以该选项错误。
选项 C: 在二叉搜索树(BST)中,确实有性质规定任何节点的左子树节点值都小于该节点值,右子树节点值都大于该节点值;而在堆中(无论是大顶堆还是小顶堆),只是要求父节点和子节点之间满足堆的大小关系(大顶堆父节点大于等于子节点,小顶堆父节点小于等于子节点),对于左子节点和右子节点之间并没有严格规定谁大谁小,左子节点可能小于也可能大于右子节点,所以该选项正确。
选项 D: 堆是一种完全二叉树结构,但说“必须是满二叉树”就不准确了,满二叉树要求每一层节点都是满的,而堆只需要是完全二叉树形态(除了最后一层节点从左到右依次排列,其他层节点数都是满的)即可,所以该选项错误。
(9)
(9)Which is wrong in the following statements ( ).
Each vertex is only visited once during the graph traversal.
There are two methods, Depth-First Search and Breadth-First Search, to traverse a graph.
Depth-First Search of a graph isn't fit to a directed graph.
Depth-first search of a graph is a recursive process.
答案:(C)
答案解释:
选项 A: 在图的遍历过程中(无论是深度优先搜索还是广度优先搜索),为了避免重复访问以及陷入死循环等情况,通常每个顶点确实只会被访问一次,会通过标记等方式来记录顶点是否已被访问过,所以该选项正确。
选项 B: 深度优先搜索(DFS)和广度优先搜索(BFS)是图遍历常用的两种基本方法,深度优先搜索沿着一条路径尽可能深地访问顶点,广度优先搜索则是按照层的顺序逐层访问顶点,所以该选项正确。
选项 C: 深度优先搜索完全适用于有向图,通过递归或者借助栈来实现对有向图的深度优先遍历,按照一定的顺序访问有向图中的顶点,所以说深度优先搜索不适合有向图是错误的,该选项符合题意。
选项 D: 深度优先搜索本质上是一个递归的过程,例如从一个起始顶点出发,递归地访问它的邻接顶点,直到不能继续深入访问时再回溯,继续探索其他分支,所以该选项正确。
Fill the blank with correct C++ codes
In order to insert a new node s after the node which pointer q points to in a circular doubly linked list, we need to execute the following statements:
s->prior=q; |
答案:q->next->prior = s; q->next = s;
答案解释:
在循环双向链表中插入节点需要正确地调整各个节点之间的指针关系,以保证链表的结构完整性以及双向可遍历性和循环特性。
当要在指针 q 所指向的节点之后插入新节点 s
时,前面已经执行了两步操作:
s->prior=q;这一步将新节点s的前驱指针指向了当前节点q,使得从s往回找能找到q。s->next=q->next;这一步将新节点s的后继指针指向了原q节点的后继节点,也就是在逻辑上把s放到了q和原q的后继节点之间的位置。
接下来还需要进行两步关键操作来完善整个插入过程:
q->next->prior = s;这一步是很重要的,因为原q的后继节点(也就是q->next所指向的节点),它的前驱指针原本是指向q的,现在要在q后面插入s,所以需要将这个后继节点(q->next)的前驱指针更新为指向新插入的节点s,这样就保证了从原q的后继节点往回找能正确找到新插入的节点s。q->next = s;最后这一步是将q节点的后继指针更新为指向新插入的节点s,使得从q往后遍历链表时能正确地访问到新插入的节点s,从而完成了整个在循环双向链表中节点插入的操作,保证链表结构依然是循环且双向可正确遍历的状态。
所以完整的插入操作需要补充
q->next->prior = s; q->next = s; 这两条语句。
Prof
that exchange sorts (Bubble sort, Selection sort, Insertion sort, etc. )
are
以下分别对冒泡排序(Bubble sort)、选择排序(Selection
sort)、插入排序(Insertion
sort)等常见交换排序在平均情况和最坏情况下时间复杂度为
冒泡排序(Bubble sort)
- 最坏情况分析:
- 原理:在最坏情况下,待排序的数组是完全逆序的。比如数组
- 对于长度为
- 根据等差数列求和公式
- 原理:在最坏情况下,待排序的数组是完全逆序的。比如数组
- 平均情况分析:
- 假设数组的所有可能排列是等概率出现的。对于任意两个元素,它们在最终排好序的位置上的先后顺序有两种可能(顺序正确或者顺序相反),且两种情况概率相等。
- 平均来说,大约一半的元素对是逆序的。而冒泡排序中交换操作的次数与逆序对的数量有关,逆序对的期望数量是
选择排序(Selection sort)
- 最坏情况分析:
- 原理:它的工作方式是每一轮从待排序元素中选择最小(或最大)的元素,然后放到已排序部分的末尾。不管输入数组是什么样的顺序,对于长度为
- 在每一轮中,为了找到最小元素,都需要遍历剩余未排序的所有元素,第一轮要遍历
- 原理:它的工作方式是每一轮从待排序元素中选择最小(或最大)的元素,然后放到已排序部分的末尾。不管输入数组是什么样的顺序,对于长度为
- 平均情况分析:
- 由于选择排序的执行步骤不依赖于输入数组元素的初始顺序(它每一轮都是固定地找最小元素等操作),无论数组初始状态如何,比较次数都固定为
- 由于选择排序的执行步骤不依赖于输入数组元素的初始顺序(它每一轮都是固定地找最小元素等操作),无论数组初始状态如何,比较次数都固定为
插入排序(Insertion sort)
- 最坏情况分析:
- 原理:在最坏情况下,比如对一个逆序的数组
- 当
- 原理:在最坏情况下,比如对一个逆序的数组
- 平均情况分析:
- 平均情况下,对于一个随机排列的数组,平均来说每个元素大约需要与前面一半的已排序元素进行比较和移动操作。对于长度为
- 平均情况下,对于一个随机排列的数组,平均来说每个元素大约需要与前面一半的已排序元素进行比较和移动操作。对于长度为
综上所述,冒泡排序、选择排序、插入排序等常见的交换排序算法在平均情况和最坏情况下时间复杂度通常是
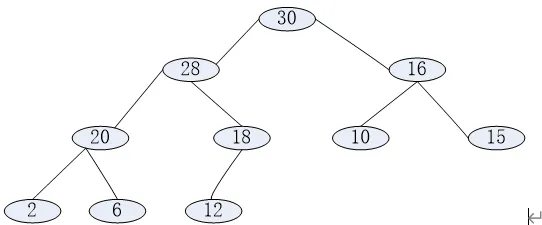
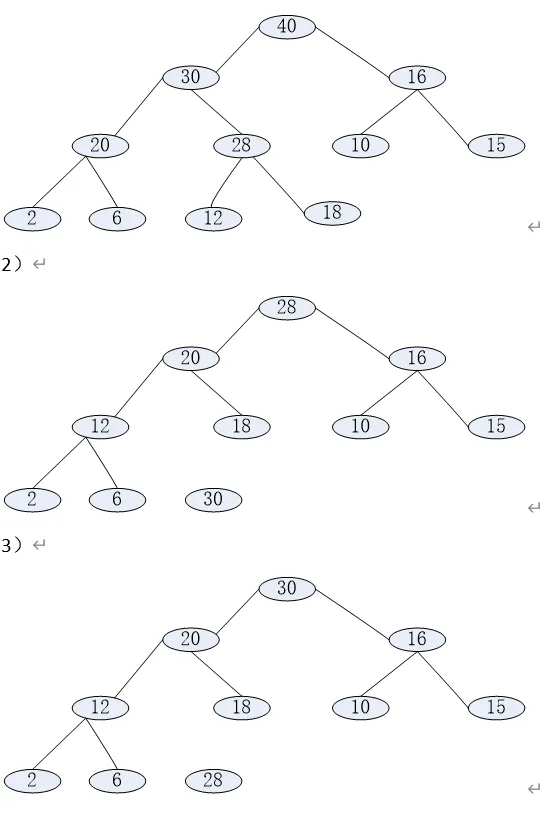
Please draw pictures to show the heaps that results from (6 scores)
adding 40 to the following heap;
deleting 30 from the following heap;
deleting 28 from the following heap.
答案解释:
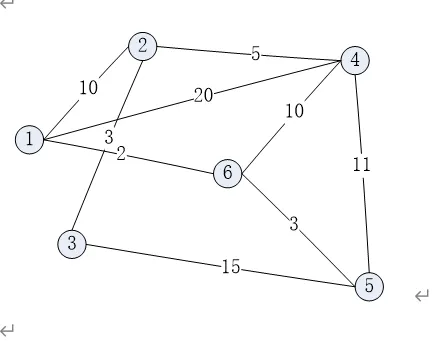
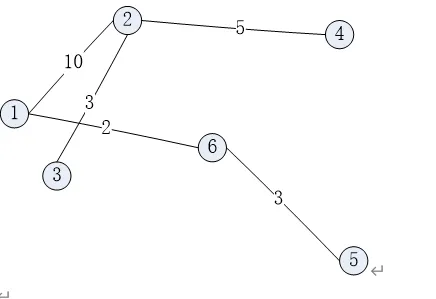
List the order in which the edges of the following graph are visited when running Prim's minimum-cost spanning tree algorithm starting at Vertex 1. Show the final MST.
答案: