离散数学考试复习整理

文件索引

Computation and Analysis (5 x 8’ = 40’)

Question

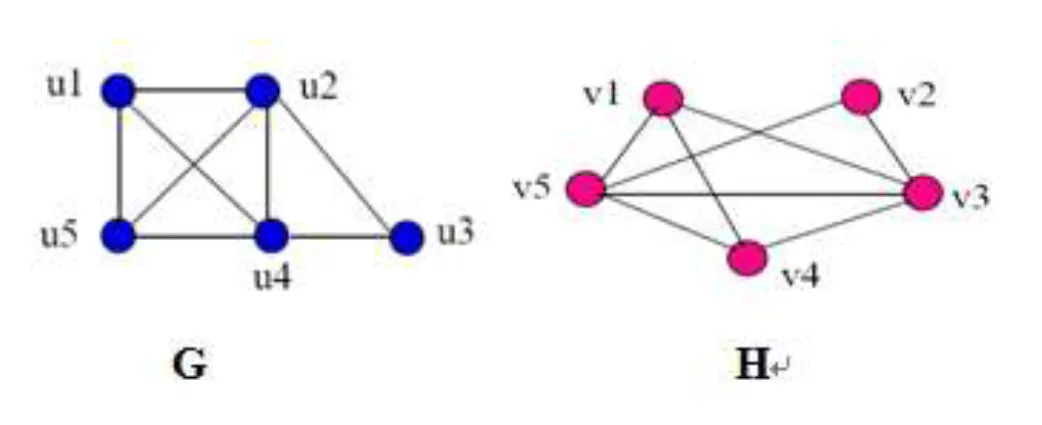
(1) Find out whether G and H are isomorphic. No matter what the judgment is, please give your explanation and argument.

Answer

deg(u3) = deg(v2) = 2 so f(u3) = v2 is our only choice. deg(u3) = deg(v2) = 2 所以 f(u3) = v2 是我们唯一的选择。
deg(u1) = deg(u5) = deg(v1 ) = deg(v4) = 3 so we must have either f(u1) = v1 and f(u5) = v4 or f(u1) = v4 and f(u5) = v1.

deg(u1) = deg(u5) = deg(v1 ) = deg(v4) = 3 所以我们必须有 f(u1) = v1 且 f(u5) = v4 或 f(u1) = v4 且 f(u5 ) = v1。
Finally since deg(u2) = deg(u4) = deg(v3) =deg(v5) = 4, we must have either f(u2) = v3 and f(u4) = v5 or f(u2) = v5 and f(u4) = v3.

最后，由于 deg(u2) = deg(u4) = deg(v3) =deg(v5) = 4，我们必须有 f(u2) = v3 且 f(u4) = v5 或 f(u2) = v5 且 f( u4) = v3。
We first try the relabeling using in each case to get the function

我们首先尝试在每种情况下使用重新标记来获取函数
f(u3)=v2, f(u1)=v1, f(u5)=v4, f(u2)=v3, f(u4)=v5. Thus, G and H are isomorphic.

f(u3)=v2，f(u1)=v1，f(u5)=v4，f(u2)=v3，f(u4)=v5。因此，G 和 H 是同构的。

解释

你描述的方法是基于顶点度数匹配的图同构判断方法，这是判断两个图是否同构的一种常用方法。具体步骤如下：

1. 根据顶点度数限制可能的映射

首先观察两个图中每个顶点的度数。由于同构图中的顶点必须具有相同的度数，因此可以先根据顶点的度数限制映射的可能性。例如，顶点 $ u_3 $ 和 $ v_2 $ 的度数都是 2，因此可以推断 $ f(u_3) = v_2 $ 是唯一的选择。

2. 递归选择可能的映射关系

接下来根据剩余顶点的度数信息进行选择。例如，$ u_1 $ 和 $ u_5 $ 的度数都是 3，可能映射到度数为 3 的顶点 $ v_1 $ 和 $ v_4 $。由于两者度数相同，映射关系有两种可能：要么 $ f(u_1) = v_1 $ 和 $ f(u_5) = v_4 $，要么 $ f(u_1) = v_4 $ 和 $ f(u_5) = v_1 $。

3. 继续递归处理剩余顶点

类似地，度数为 4 的顶点 $ u_2 $ 和 $ u_4 $ 也可以映射到度数为 4 的 $ v_3 $ 和 $ v_5 $，根据同样的逻辑进行两种可能的映射选择。

4. 尝试映射并验证

然后对每一种映射情况进行尝试，并构造函数 $ f $ 来映射顶点。例如，尝试 $ f(u_3) = v_2 $, $ f(u_1) = v_1 $, $ f(u_5) = v_4 $, $ f(u_2) = v_3 $, $ f(u_4) = v_5 $。

在映射过程中，验证每个顶点及其邻居之间的连接关系是否一致。如果一致，证明两个图是同构的。

总结

这种方法依赖于顶点的度数来减少映射的可能性，逐步缩小顶点映射的选择范围，直到最终构建出一个同构映射。该方法不需要遍历所有可能的顶点排列，而是通过度数信息来减少复杂度，属于一种启发式的图同构检测方法。

Question

证明：$(\forall x)(P(x) \rarr Q(x)) \rarr ((\exist x)P(x) \rarr(\exist x)Q(x))$ is a tautology

Answer

当然，让我们逐步详细解释这张图中的逻辑推导过程，说明每一步所使用的逻辑规则和简化过程。

初始表达式：

$ x (P(x) Q(x)) (x P(x) x Q(x)) $

这个表达式可以用自然语言理解为：

如果对于所有 $x$，$P(x)$ 蕴含 $Q(x)$（即每个 $x$ 满足 $P(x)$ 的同时也满足 $Q(x)$），

那么，如果存在某个 $x$ 使得 $P(x)$ 为真，则也存在某个 $x$ 使得 $Q(x)$ 为真。

这是一个典型的蕴含命题，涉及全称量词、存在量词和命题逻辑中的蕴含（$\to$）。

第一步：去掉蕴含符号

$ x (P(x) Q(x)) (x P(x) x Q(x)) $

细节说明：

首先使用逻辑等价式将 $(P(x) \to Q(x))$ 转换为 $(\neg P(x) \lor Q(x))$。这是因为 $P(x) \to Q(x)$ 在逻辑上等价于 $\neg P(x) \lor Q(x)$（蕴含的等价转换）。

然后处理整个表达式的左侧 $\forall x (P(x) \to Q(x))$，将其变为 $\neg \forall x (\neg P(x) \lor Q(x))$（全称量词的否定）。根据德·摩根定律，$\neg \forall x A(x)$ 等价于 $\exists x \neg A(x)$，但这一步暂时保持$\neg \forall x$不变。

处理右侧的蕴含 $(\exists x P(x) \to \exists x Q(x))$，将其转换为 $\neg \exists x P(x) \lor \exists x Q(x)$（蕴含的等价转换）。

第二步：应用量词的逻辑规则

$ x (P(x) Q(x)) x Q(x) x P(x) $

细节说明：

使用德·摩根定律将左侧 $\neg \forall x (\neg P(x) \lor Q(x))$ 转换为 $\exists x (P(x) \land \neg Q(x))$。因为 $\neg \forall x A(x)$ 等价于 $\exists x \neg A(x)$，并且 $\neg (\neg P(x) \lor Q(x))$ 等价于 $P(x) \land \neg Q(x)$。

右侧 $\neg \exists x P(x) \lor \exists x Q(x)$ 保持不变。

第三步：合并量词

$ x ((P(x) Q(x)) Q(x)) x P(x) $

细节说明：

对左侧的两个存在量词 $\exists x (P(x) \land \neg Q(x))$ 和 $\exists x Q(x)$ 进行简化。由于 $\exists x Q(x)$ 代表存在一个 $x$ 使 $Q(x)$ 成立，它可以并入到前面的表达式里。于是将整个部分合并为 $\exists x ((P(x) \land \neg Q(x)) \lor Q(x))$。

保持右侧的 $\neg \exists x P(x)$ 不变。

第四步：简化内部表达式

$ x (P(x) Q(x)) x P(x) $

细节说明：

观察到 $(P(x) \land \neg Q(x)) \lor Q(x)$ 可以进一步简化为 $P(x) \lor Q(x)$。这是因为对于任意 $x$，要么 $Q(x)$ 成立，要么 $P(x)$ 成立。如果 $Q(x)$ 成立，整个表达式成立；如果 $Q(x)$ 不成立，只有 $P(x)$ 为真时才能使表达式成立。所以 $(P(x) \land \neg Q(x)) \lor Q(x)$ 就等价于 $P(x) \lor Q(x)$。

左侧的存在量词部分现在简化为 $\exists x (P(x) \lor Q(x))$，右侧部分保持不变。

第五步：分配存在量词

$ x P(x) x Q(x) x P(x) $

细节说明：

进一步将 $\exists x (P(x) \lor Q(x))$ 分配为两个独立的存在量词表达式：$\exists x P(x)$ 和 $\exists x Q(x)$。这一步基于逻辑规则，即 $\exists x (P(x) \lor Q(x))$ 等价于 $\exists x P(x) \lor \exists x Q(x)$。

最终我们得到 $\exists x P(x) \lor \exists x Q(x) \lor \neg \exists x P(x)$。

最后一步：恒真式

$ 1 $

细节说明：

现在，我们有 $\exists x P(x)$ 和 $\neg \exists x P(x)$，它们是互补的（互为否定）。这意味着不管 $P(x)$ 是否存在，总有一个为真。因此，$\exists x P(x) \lor \neg \exists x P(x)$ 恒为真。

因此，整个表达式成为一个恒真命题，即逻辑值为 $1$。

结论：

通过一系列逻辑变换和简化，我们证明了初始命题是恒真的，即不管 $P(x)$ 和 $Q(x)$ 取何种值，命题总是成立。这是一种典型的逻辑推导过程，使用了量词的规则（如德·摩根定律、存在量词和全称量词的否定转换）以及蕴含的等价形式等。

Question

Construct an argument using rules of inference to show that the hypotheses:

“Ellen, a student in this class, owns a red convertible. Everyone who owns a red convertible has gotten at least one speeding ticket.”
imply the conclusion “someone in this class has gotten a speeding ticket.”

使用推理规则构造一个论证来表明假设：

“艾伦，这个班的学生，拥有一辆红色的敞篷车。每个拥有红色敞篷车的人都至少经历过一次超速驾驶。暗示结论“这个班级中有人收到了超速罚单”。

Answer

Solution 1

这个图展示了一个一阶逻辑的推导过程，涉及几个谓词符号和量词操作。让我们详细解释每个部分：

1. 定义：

S(x): $x$ 是这个班级的学生（x is a student in this class）。

R(x): $x$ 是一辆红色敞篷车（x is a red convertible）。

O(x, y): $x$ 拥有 $y$（x owns y）。

T(x): $x$ 是一张超速罚单（x is a speeding ticket）。

讨论的领域 $x, y, z$ 都是所有的人或物品。

2. 假设：

H1: $S(Ellen) \land \exists y (R(y) \land O(Ellen, y))$

意思是：Ellen 是学生，且存在一个 $y$，使得 $y$ 是红色敞篷车，Ellen 拥有这个车。

H2: $\forall x (\exists y (O(x, y) \land R(y)) \to \exists z (T(z) \land O(x, z)))$

意思是：对所有的 $x$，如果 $x$ 拥有一个红色敞篷车，那么 $x$ 必定拥有一张超速罚单。

C（结论）: $\exists x \exists y (S(x) \land T(y) \land O(x, y))$

意思是：存在某个人 $x$ 和某个物体 $y$，使得 $x$ 是学生，$y$ 是超速罚单，且 $x$ 拥有 $y$。

3. 证明：

使用假设 H2 通过普遍实例化（Universal Instantiation, UI）对 $x = Ellen$：

$\exists y (O(Ellen, y) \land R(y)) \to \exists z (T(z) \land O(Ellen, z))$

意思是：如果 Ellen 拥有一个红色敞篷车，那么 Ellen 拥有一张超速罚单。

根据 H1，我们知道 Ellen 拥有一个红色敞篷车，即 $\exists y (O(Ellen, y) \land R(y))$ 为真。

结合 H1 和 H2，我们可以使用存在实例化（Existential Instantiation, EI）得出：存在一个 $z$，使得 $T(z) \land O(Ellen, z)$ 为真。也就是说，存在某个 $z$ 是超速罚单，且 Ellen 拥有这个罚单。

最终，由于 Ellen 是学生，结合以上推理，可以得出结论 $C$：存在某个人（Ellen）和某个物体（超速罚单 $z$），使得 Ellen 是学生，且她拥有一张超速罚单。

4. 逻辑推导总结：

H1 确定 Ellen 是一个学生，并且拥有一辆红色敞篷车。

H2 通过条件推理，表明拥有红色敞篷车的人也拥有超速罚单。

通过这两条假设的结合，我们证明了 Ellen 拥有超速罚单，从而推导出最终结论 $C$。

这整个推导过程依赖于一阶逻辑的普遍实例化和存在实例化规则，以及条件推理和量词的使用。

Solution 2

这个逻辑表达涉及对谓词逻辑的推理，包含定义、前提和结论。让我们逐步解析：

1. 定义：

S(x): $x$ 是这个班级的学生（$x$ is a student in this class）。

C(x): $x$ 拥有一辆红色敞篷车（$x$ owns a red convertible）。

P(x, y): $x$ 得到了一张超速罚单 $y$（$x$ has gotten a speeding ticket $y$）。

T(x): $x$ 是一张超速罚单（$x$ is a speeding ticket）。

2. 结论（推导目标）：

"班级中有人得到了超速罚单"（someone in this class has gotten a speeding ticket）。这意味着最终我们要证明存在某个 $x$ 和某个 $y$，使得 $x$ 是学生，$y$ 是超速罚单，且 $x$ 拥有这个罚单。

3. 前提：

S(Linda) ∧ C(Linda): Linda 是这个班级的学生，并且拥有一辆红色敞篷车。

$\forall x (C(x) \to \exists y (T(y) \land P(x, y)))$: 对所有 $x$，如果 $x$ 拥有一辆红色敞篷车，则存在某个 $y$，使得 $y$ 是超速罚单，且 $x$ 得到这张罚单。

4. 结论：

$\exists x \exists y [S(x) \land T(y) \land P(x, y)]$: 结论是，存在某个 $x$ 和 $y$，使得 $x$ 是学生，$y$ 是超速罚单，且 $x$ 拥有这张罚单。

5. 证明推理：

Step 1: 根据前提 $S(Linda) \land C(Linda)$，我们知道 Linda 是学生，并且拥有一辆红色敞篷车。

Step 2: 根据 $\forall x (C(x) \to \exists y (T(y) \land P(x, y)))$，我们应用普遍实例化（UI，Universal Instantiation），对 $x = Linda$：

由于 $C(Linda)$ 为真（Linda 拥有红色敞篷车），我们得出 $\exists y (T(y) \land P(Linda, y))$，即存在某个 $y$，使得 $y$ 是超速罚单，且 Linda 得到这张罚单。

Step 3: 从以上推理得出，存在某个超速罚单 $y$，且 Linda 得到了这张罚单，同时 Linda 是学生。这意味着：

存在 $x = Linda$ 和 $y$，使得 $S(x) \land T(y) \land P(x, y)$ 为真。

因此，我们得出了结论：班级中有一个学生（Linda）得到了超速罚单。

总结：

该推导基于一阶逻辑的普遍实例化（UI）和存在实例化（EI），结合前提 $S(Linda)$ 和 $C(Linda)$ 以及条件推理，得出了最终结论，即存在一个学生得到了超速罚单。

Question

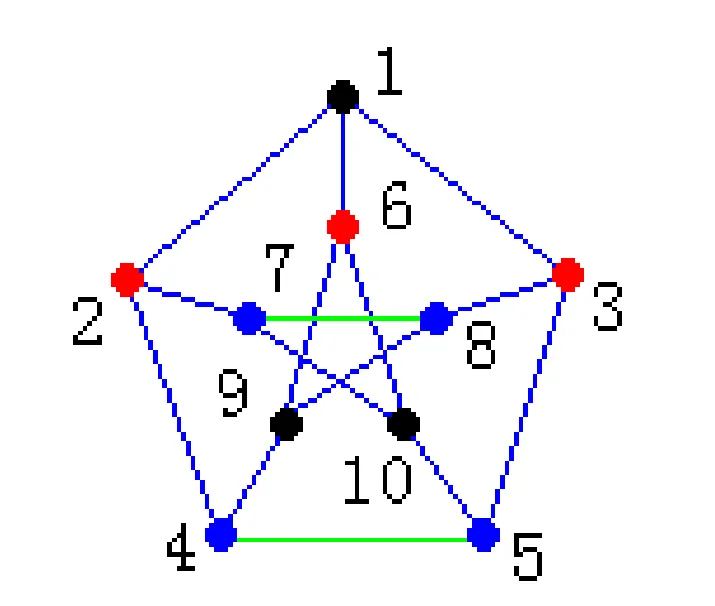
Prove that Petersen graph is non-planar graphs.

证明Petersen图是非平面图。

Answer

（需要后续修改一下）

The sub-graph H of the Petersen shown in Figure (b) obtained by deleting 3 and the three edges that have 3 as an endpoint,

图(b)所示的Petersen子图H是删除3以及以3为端点的3条边得到的，
is homeomorphic to K3,3.

与 K3,3 同胚。
Hence, the Petersen graph is non-planar.

因此，Petersen 图是非平面的。

Question

Show that the relation R on the set of all bit strings such that s R t if and only if s and t contain the same odd- or even-property number of 1s is an equivalence relation. (For example, one has 2 1s and the other also has even number of 1s )

证明所有位串集合上的关系R 使得s R t 当且仅当s 和t 包含相同的奇数或偶数属性1 时，才是等价关系。（例如一个有2个1，另一个也有偶数个1）

Answer

x R x，S is reflexive.

x R x，S 是自反的。
If x R y, they have odd (or even) number of 1s, Hence, y R x, symmetric.

若 x R y 中 1 的个数为奇数（或偶数），则 y R x 对称。
If x R y and y R z, R is transitive.

如果x R y 和y R z ，R 是传递性的。

Application of Discrete Mathematics. (5 x 12’ = 50’)

Question

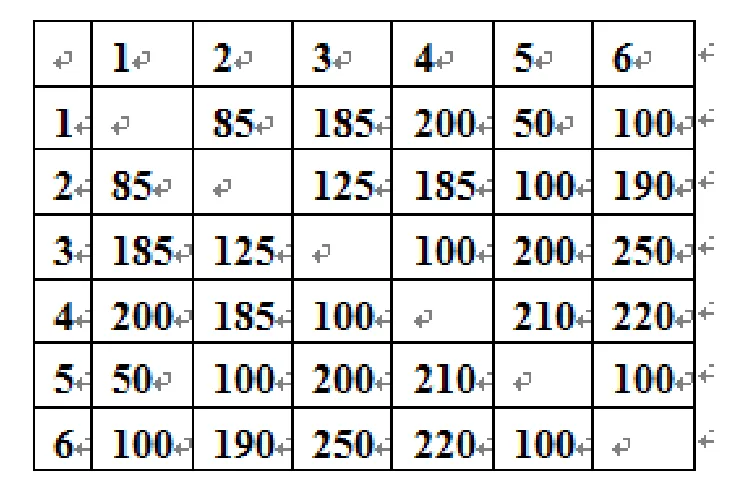
How many different channels are needed for six stations located at the distances shown in the table, if two stations can not use the same channel when they are within 180 miles of each other?

如果两个电台在相距 180 英里以内时不能使用同一信道，那么位于表中所示距离的 6 个电台需要多少个不同的信道？

Answer

Solution: This schedule problem can be solved using a graph model, with vertices representing stations and with edges between two vertices if the distances are within 180 miles. Chromatic number is 3.

解决方案：这个调度问题可以使用图模型来解决，其中顶点代表车站，如果距离在 180 英里以内，则两个顶点之间有边。色数为3。

Question

If a person is a university student, he is either a liberal-arts student or a science student.

Some university student is an outstanding student. John is not a liberal-arts student, but he is an outstanding student.
John is a university student.
Use rules of inference to show that John is a science student.

如果一个人是大学生，他要么是文科学生，要么是理科学生。有些大学生是一名优秀的学生。约翰不是文科生，但他是一名优秀的学生。

约翰是一名大学生。使用推理规则表明约翰是一名理科学生。

Answer

这是一个逻辑推理题的解答过程。

首先，给出了一些定义： $P(x)$表示$x$是一名大学生。 $Q(x)$表示$x$是一名文科生。 $S(x)$表示$x$是一名理科生。 $T(x)$表示$x$是一名优秀学生。

接着给出了三个前提条件： $(∀x)P(x) → (Q(x) ∨ S(x))$，表示所有大学生都是文科生或理科生。 $(∃x)P(x) ∧ T(x)$，表示存在一名既是大学生又是优秀学生的同学。 $¬Q(c) ∧ T(c)$，表示John不是文科生，并且他是一名优秀学生。 $P(c)$，表示John是大学生。

根据这些信息，我们可以进行以下推断：

$(∀x)P(x)→(Q(x)∨S(x))$ 是一个全称命题，表示对于所有的x，如果x是大学生，则x是文科生或者理科生。
$P(c)→(Q(c)∨S(c))$ 是通过通用量化引入（Universal Quantifier Introduction, US）从①得到的，表示如果c是大学生，则c是文科生或者理科生
$P(c)$ 表示c是大学生，这是给定的前提之一。
$Q(c)∨S(c)$ 是通过②和③使用蕴含引入（Implication Introduction, →I）得到的，表示如果c是大学生，则c是文科生或者理科生。
$¬Q(c)∧T(c)$ 是给定的前提之一，表示c不是文科生并且c是优秀学生。
$¬Q(c)$ 是通过⑤使用析取否定引入（Disjunctive Syllogism, DS）得到的，表示c不是文科生。
$S(c)$ 是通过④和⑥使用析取分离（Disjunction Elimination, ∨E）得到的，表示c是理科生。

因此，结论是 John 是一名理科生。

Question

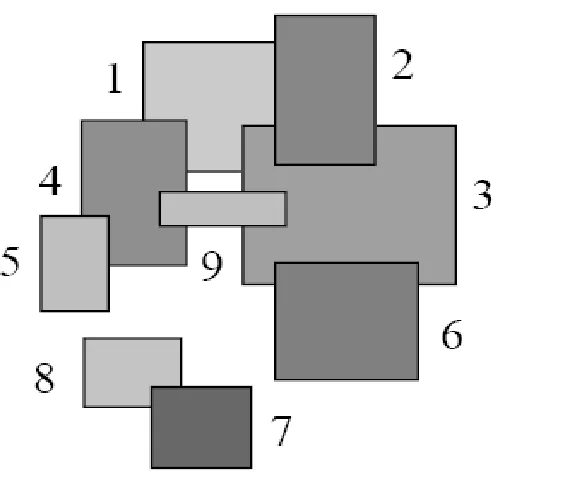
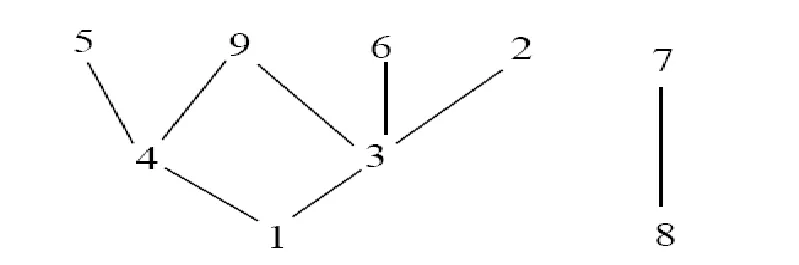
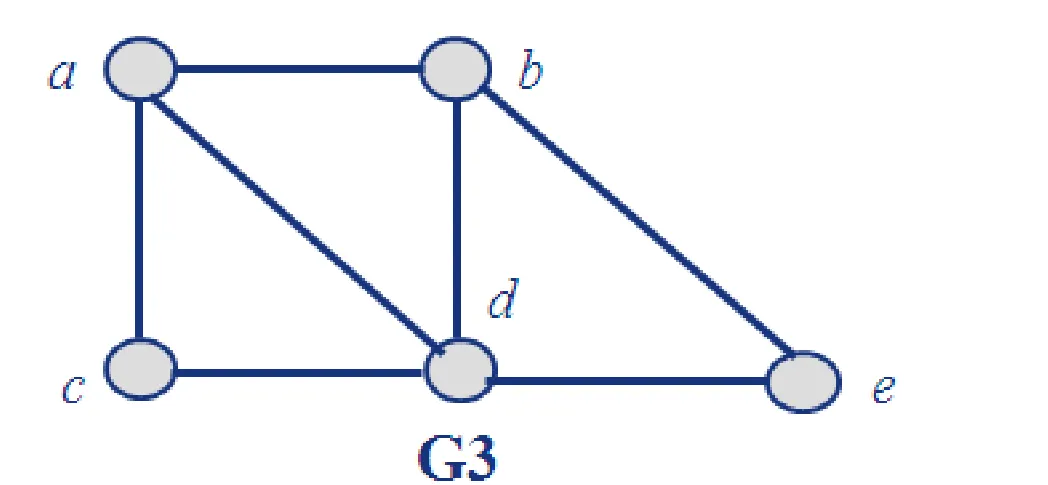
Consider the rectangles T={1,…,9} and the relation R such that i R j = “i is more distant than j from the viewer.” Then R is a partial order on the set of rectangles. Please show an order of topological sorting according to the following figure.

Answer

Then 1R2, 1R4, 1R3, 4R9, 4R5, 3R2, 3R9, 3R6, 8R7.

然后是 1R2、1R4、1R3、4R9、4R5、3R2、3R9、3R6、8R7。
The Hasse diagram for R is

R 的哈斯图是
An order of topological sorting is “1 4 3 8 5 9 6 2 7”.

拓扑排序的顺序为“1 4 3 8 5 9 6 2 7”。

Question

n cities are connected by k roads. A road is incident with only two cities, which is defined as an edge between two vertices (cities).

A property of the roads and cities is k>(n-1)(n-2)/2.
The question is whether people can travel between any two cities through the roads.

n 个城市由 k 条道路连接。一条道路只与两个城市相交，定义为两个顶点（城市）之间的边。道路和城市的属性是k>(n-1)(n-2)/2。问题是人们是否可以通过道路在任意两个城市之间出行。

Answer

Supposed that a graph of the given n cities and k roads is G, the question can be considered to be the proof that G is= connected.

假设给定的n个城市和k条道路的图是G，则该问题可以认为是G是连通的证明。
Given simple graph G=(V,E), |V|=n cities and|E|=k roads, please prove that G is connected when k>(n-1)(n-2)/2.

给定简单图G=(V,E)，|V|=n个城市和|E|=k条道路，请证明当k>(n-1)(n-2)/2时G是连通的。
Supposed that G is unconnected, G has at least 2 connected component, signed as G1=(V1, E1) and G2=(V2, E2), where |V1|=n1, |V2|=n2 and n1+n2=n.

假设G 不连通，G 至少有2 个连通分量，符号为G1=(V1, E1) 和G2=(V2, E2)，其中|V1|=n1，|V2|=n2 和n1+n2=n
Because G is a simple graph, |E1|<=n1(n1-1)/2 and |E2|<=n2(n2-1)/2.

因为 G 是简单图，|E1|<=n1(n1-21)/2 且 |E2|<=n2(n2-1)/2。
Therefore, k<=n1(n1-1)/2+n2(n2-1)/2.

因此，k<=n1(n1-1)/2+n2(n2-1)/2。
Since n1<=n-1 and n2<=n-1, k<=(n-1)(n1-1+n2-1)=(n-1)(n-2)/2.

由于n1<=n-1 且n2<=n-1，因此k<=(n-1)(n1-1+n2-1)=(n-1)(n-2)/2。
This is contradictory to the condition that k>(n-1)(n-2)/2.

这与k>(n-1)(n-2)/2的条件矛盾。
Thus, G is connected, so people can travel between any two cities through the roads.

这样，G是连通的，人们可以通过道路在任意两个城市之间出行。

Answer of Quiz 3

Question

Can the following graph be drawn in one stroke ? 能否一笔画出下面的图形？

Answer

The degrees of vertex a and b of graph G are odd, and the degrees of other vertices are even, which is following the sufficient condition of Euler path. Thus, G be drawn in one stroke.

图G的顶点a和b的度数为奇数，其他顶点的度数为偶数，满足以下充分条件欧拉路径。这样，G就一笔画出来了。

Theorem 2: A connected graph has an Euler path but not an Euler circuit if and if only if it has exactly two vertices of odd degree.

定理 2：连通图有欧拉路径，但没有欧拉路径，欧拉电路当且仅当它恰好有两个奇数顶点程度。

Question

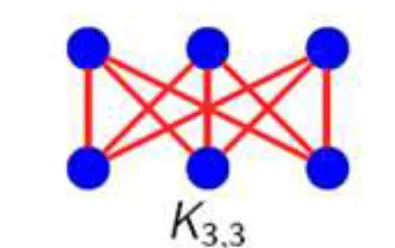
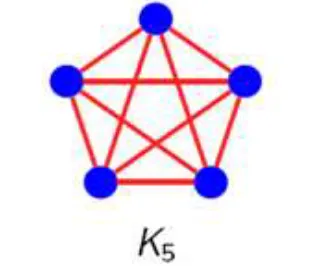
Prove that K5 and K3,3 are non-planar graphs.

证明 K5 和 K3,3不是平面图。

Answer

Proof. (1) Supposed K5 is planar, $r = e – v + 2 $according to Euler formula.
Since each region has degree greater than or equal to three, it follows that $2e = \sum deg(R) \geq 3r$。
$2e/3>=e – v + 2$. Thus, $e<=3v-6.$
For K5, $e=10$ and $v=5$, so K5 is non-planar.
Proof. (2) Supposed K3,3 is planar, $r = e – v + 2$ according to Euler formula
Since each region has degree greater than or equal to three, it follows that $2e>=4r$
$e/2>=e – v + 2$. Thus, $e<=2v-4$.
For K5, $e=9$ and $v=6$, so K5 is non-planar.

Question

Prove that there are three persons who know each other or don’t know each other in every six persons in the world.

Answer

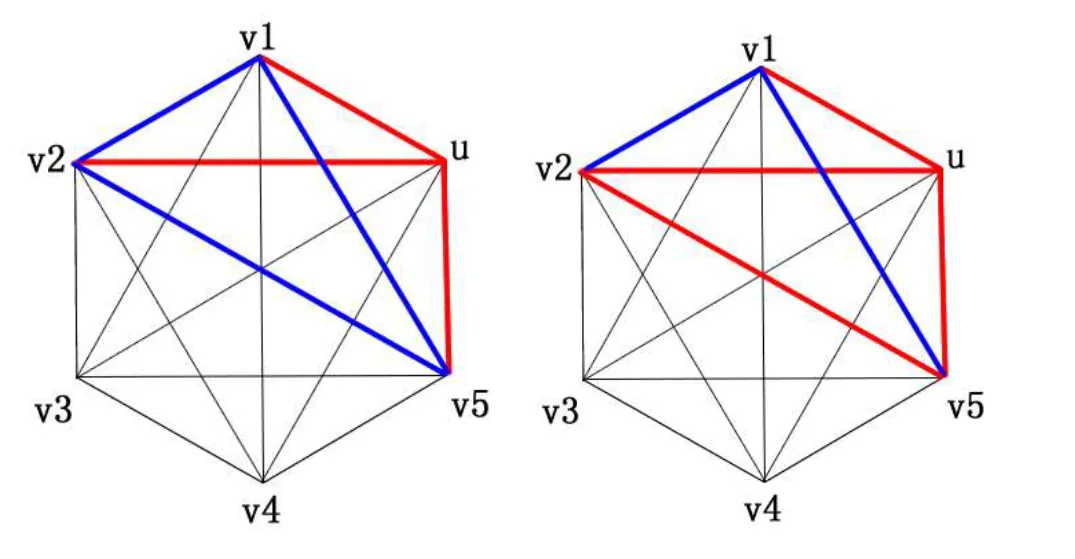
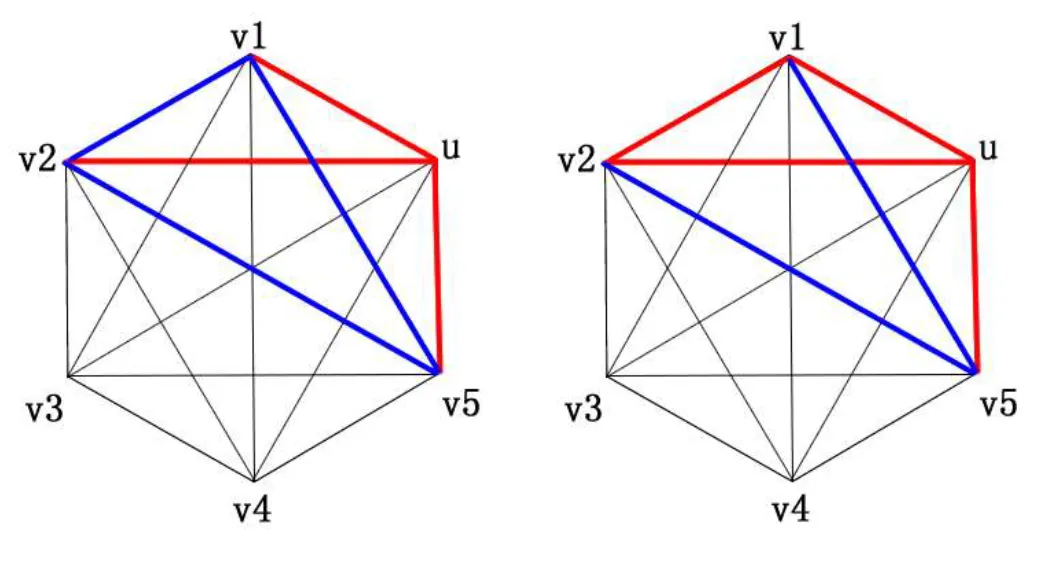
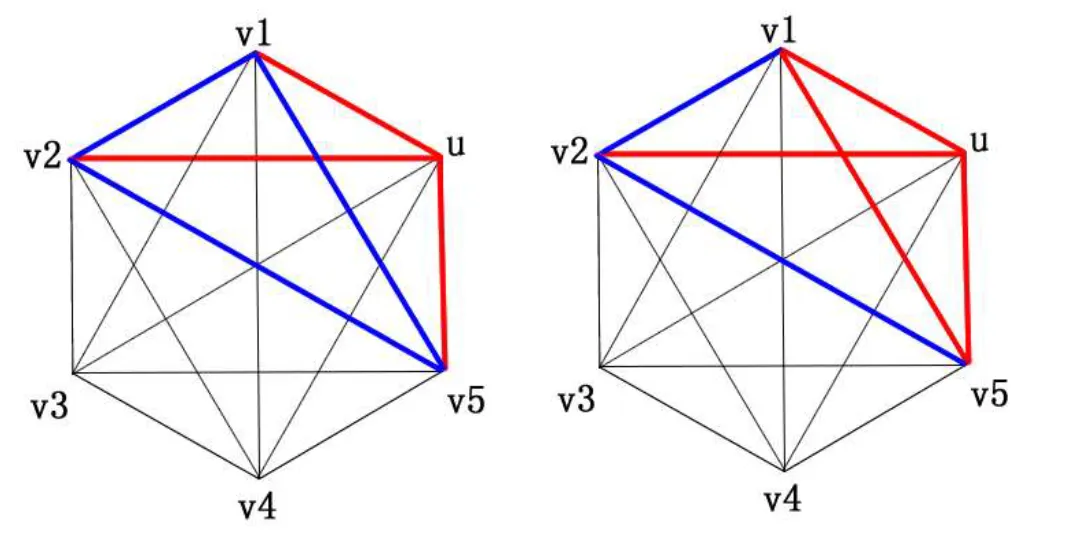
Proof. Six vertices represent six persons. If two persons know each other, the edge between the vertices is colored in red. Otherwise, the edge is colored in blue.
The problem is changed to prove that K6 can be colored to be a red K3 and blue K3.
In K6, vertex u is incident with 5 edges.
According to drawer principle, there are at least 3 edges colored in the same.
Supposed (u, v1), (u, v2) and (u,v5) are colored in red,
consider the color of edges (v1, v2), (v1, v5) and (v2, v5).

Question

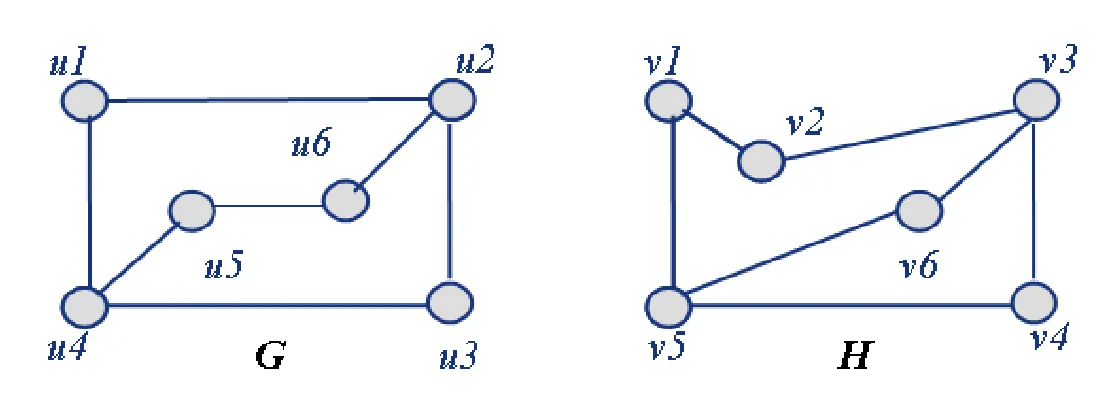
Find out whether G and H are isomorphic. No matter what the judgment is, please give your explanation and argument.

Answer

Solution: They are isomorphic. The isomorphism is: f(u1)=v6, f(u2)=v3, f(u3)=v4, f(u4)=v5, f(u5)=v1, f(u6)=v2

解：它们是同构的。同构为：f(u1)=v6、f(u2)=v3、f(u3)=v4、f(u4)=v5、f(u5)=v1、f(u6)=v2

离散数学考试复习整理

文件索引

Computation and Analysis (5 x 8’ = 40’)

Question

(1) Find out whether G and H are isomorphic. No matter what the judgment is, please give your explanation and argument.

Answer

解释

1. 根据顶点度数限制可能的映射

2. 递归选择可能的映射关系

3. 继续递归处理剩余顶点

4. 尝试映射并验证

总结

Question

证明：\((\forall x)(P(x) \rarr Q(x)) \rarr ((\exist x)P(x) \rarr(\exist x)Q(x))\) is a tautology

Answer

初始表达式：

第一步：去掉蕴含符号

细节说明：

第二步：应用量词的逻辑规则

细节说明：

第三步：合并量词

细节说明：

第四步：简化内部表达式

细节说明：

第五步：分配存在量词

细节说明：

最后一步：恒真式

细节说明：

结论：

Question

Construct an argument using rules of inference to show that the hypotheses:

Answer

Solution 1

1. 定义：

2. 假设：

3. 证明：

4. 逻辑推导总结：

Solution 2

1. 定义：

2. 结论（推导目标）：

3. 前提：

4. 结论：

5. 证明推理：

总结：

Question

Prove that Petersen graph is non-planar graphs.

Answer

Question

Show that the relation R on the set of all bit strings such that s R t if and only if s and t contain the same odd- or even-property number of 1s is an equivalence relation. (For example, one has 2 1s and the other also has even number of 1s )

Answer

Application of Discrete Mathematics. (5 x 12’ = 50’)

Question

How many different channels are needed for six stations located at the distances shown in the table, if two stations can not use the same channel when they are within 180 miles of each other?

Answer

Question

If a person is a university student, he is either a liberal-arts student or a science student.

Some university student is an outstanding student. John is not a liberal-arts student, but he is an outstanding student.

John is a university student.

Use rules of inference to show that John is a science student.

Answer

Question

Consider the rectangles T={1,…,9} and the relation R such that i R j = “i is more distant than j from the viewer.” Then R is a partial order on the set of rectangles. Please show an order of topological sorting according to the following figure.

Answer

Question

n cities are connected by k roads. A road is incident with only two cities, which is defined as an edge between two vertices (cities).

A property of the roads and cities is k>(n-1)(n-2)/2.

The question is whether people can travel between any two cities through the roads.

Answer

Answer of Quiz 3

Question

Can the following graph be drawn in one stroke ? 能否一笔画出下面的图形？

Answer

Question

Prove that K5 and K3,3 are non-planar graphs.

Answer

Question

Prove that there are three persons who know each other or don’t know each other in every six persons in the world.

Answer

Question

Find out whether G and H are isomorphic. No matter what the judgment is, please give your explanation and argument.