DIS02AB
DIS02AB
1. 稳定匹配
考虑工作集合\(J = \{1,2,3\}\)和候选人集合\(C = \{A,B,C\}\),具有以下偏好。
| 工作 | 候选人 |
|---|---|
| 1 | \(A > B > C\) |
| 2 | \(B>A > C\) |
| 3 | \(A > B > C\) |
| 候选人 | 工作 |
|---|---|
| \(A\) | \(2>1 > 3\) |
| \(B\) | \(1>3 > 2\) |
| \(C\) | \(1>2 > 3\) |
在这个例子上运行传统的求婚与拒绝算法。它需要多少天,最终的配对是什么?(展示你的计算过程。)
解决方案:
该算法需要 5 天来产生一个匹配。最终的配对如下。圆圈表示候选人在某一天选择的工作(并拒绝了其他工作)。\(\{(A,2),(B,1),(C,3)\}\)
| 候选人 | 第 1 天 | 第 2 天 | 第 3 天 | 第 4 天 | 第 5 天 |
|---|---|---|---|---|---|
| \(A\) | \(\boxed{1}3\) | \(\boxed{1}\) | \(1,\boxed{2}\) | \(\boxed{2}\) | \(\boxed{2}\) |
| \(B\) | \(\boxed{2}\) | \(2,\boxed{3}\) | \(\boxed{3}\) | \(\boxed{1},3\) | \(\boxed{1}\) |
| \(C\) | \(\boxed{3}\) |
原理:
偏好列表:假设有两组参与者,例如男性集合\(M\)和女性集合\(W\),每个参与者对另一组的成员都有一个严格的偏好排序。
匹配过程:
- 初始时,所有人都是未婚状态。
- 在每一轮中,每个未婚男性向他偏好列表中尚未拒绝他的最高排名的女性求婚。
- 女性收到求婚请求后,如果她当前未婚,或者求婚者比她当前的未婚夫在她的偏好列表中排名更高,她就会暂时接受求婚(即拒绝当前未婚夫,如果有的话),否则拒绝求婚。
- 这个过程持续进行,直到没有更多的求婚发生,此时算法终止,得到一个稳定匹配。
- 注意最后终止一定是有一个女性被最后求婚,也是她收到的唯一一次求婚。
首先,这里工作是\(M\),候选人是\(W\):
第一轮:1 找 A,A 暂时接收;然后 2 找 B,B 暂时接受;3 找 A,由于在 A 心目中 1>3,所以 3 被 A 拒绝,第一轮结束,结果为\((1,A),(2,B),(3,no)\)。
第二轮:由于只有 3 没找到,所以 3 从没有拒绝的候选人中继续寻找:3 找 B,在 B 心目中 3>2,所以 3 被 B 接受,2 被 B 拒绝,第二轮结束。结果为\((1,A),(2,no),(3,B)\)
第三轮:找 2 的对应匹配,因为 B 已经拒绝过 2,所以 2 找 A,在 A 心目中 2>1,所以 2 被 A 接受,1 被 A 拒绝,第三轮结束。结果为\((1,no),(2,A),(3,b)\)
第四轮:找 1 的对应匹配,因为 A 已经拒绝过 1,所以 1 找 B,在 B 心目中 1>3,所以 1 被 B 接受,3 被 B 拒绝,第四轮结束。结果为\((1,B),(2,A),(3,no)\)
第五轮:找 3 的对应匹配,因为 A,B 已经拒绝过 3,所以 3 找 C,由于 C 为空,所以接受 3,第五轮结束。结果为\((1,B),(2,A),(3,C)\),到此全部结束。
2. 求婚与拒绝算法的证明
证明关于传统求婚与拒绝算法的以下陈述。
- 在算法的任何执行过程中,如果候选人在第\(i\)天收到求婚,那么在之后的每一天直到算法终止他们都会收到求婚。
- 在算法的任何执行过程中,如果候选人在第\(i\)天没有收到求婚,那么在之前的任何一天\(j\)(\(1\leq j < i\))他们也没有收到求婚。
- 在算法的任何执行过程中,至少有一个候选人只收到一个求婚。(提示:使用上面的部分!)
解决方案:
- 思路是对迄今为止经过的天数进行归纳。
- 基础情形:候选人\(C\)在第\(i\)天收到求婚。
- 归纳步骤:假设\(C\)在第\(j\geq i\)天从工作\(J\)收到求婚。我们要证明他们在第\(j + 1\)天也会收到求婚。有两种情况:\(C\)更喜欢\(J\)胜过其他所有求婚,或者\(C\)更喜欢某个工作\(J'\)胜过\(J\)。在第一种情况下,\(J\)在第\(j + 1\)天向\(C\)求婚,在第二种情况下,\(J'\)在第\(j + 1\)天向\(C\)求婚,所以\(C\)在第\(j + 1\)天至少收到一个求婚。
- 一种方法是使用反证法。假设候选人在第\(i\)天没有收到求婚,但在之前的某一天\(j\)(\(1\leq j < i\))收到了求婚。根据上一部分,由于候选人在第\(j\)天收到了求婚,他们在\(j\)天后的每一天都必须至少收到一个求婚。但是\(i > j\),所以候选人在第\(i\)天一定收到了求婚,这与我们最初假设他们没有收到求婚相矛盾。
- 假设算法需要\(k\)天。这意味着每个候选人在第\(k\)天都必须收到求婚。然而,这也意味着至少有一个候选人\(C\)在第\(k - 1\)天没有收到求婚——如果不是这样,算法在第\(k - 1\)天就已经终止了。然后根据(b)部分,由于\(C\)在第\(k - 1\)天没有收到求婚,他们在\(k\)天之前的任何一天都没有收到求婚。此外,我们知道他们在第\(k\)天恰好收到一个求婚,因为算法在那天终止了。因此,我们得到\(C\)在整个算法运行过程中恰好收到一个求婚。
3. 做评判
通过稳定匹配实例,我们指的是一组工作和候选人以及他们的偏好列表。对于以下每个陈述,指出该陈述是真还是假,并给出一个简短的 2 - 3 行解释来证明你的答案:
- 对于\(n > 1\),存在一个\(n\)个工作和\(n\)个候选人的稳定匹配实例,使得在工作求婚的稳定匹配算法中,每个工作最终都与它最不喜欢的候选人配对。
- 在稳定匹配实例中,如果工作\(J\)和候选人\(c\)都将对方放在各自偏好列表的首位,那么在每个稳定配对中\(J\)必须与\(c\)配对。
- 在至少有两个工作和两个候选人的稳定匹配实例中,如果工作\(J\)和候选人\(C\)都将对方放在各自偏好列表的底部,那么在任何稳定配对中\(J\)都不能与\(C\)配对。
- 对于每个\(n > 1\),存在一个\(n\)个工作和\(n\)个候选人的稳定匹配实例,其中有一个不稳定配对,使得每个未匹配的工作 - 候选人对都是不稳定对或配对。
解决方案:
- 假:如果发生这种情况,这意味着在算法结束时,每个工作都向其列表上的每个候选人求婚并且被拒绝了\(n - 1\)次。这也意味着每个候选人都收到了每个工作的求婚,并且在最后一天必须总共拒绝了\(n - 1\)个工作(以便最终只剩下一个更喜欢的工作)。然而,我们知道这是不可能的,正如我们上面所学,至少有一个候选人只收到一个求婚。因此,必须至少有一个候选人直到最后一天才收到求婚。
- 真:我们通过简单的反证法证明。假设\(J\)和\(C\)将对方放在各自偏好列表的首位,但在某个稳定配对\(S\)中\(J\)和\(C\)没有配对。因此,\(S\)包括配对\((J,C')\),\((J',C)\),对于某个工作\(J'\)和候选人\(C'\)。然而,\(J\)更喜欢\(C\)胜过其在\(S\)中的伙伴,因为\(C\)在\(J\)的偏好列表顶部。类似地,\(C\)更喜欢\(J\)胜过她当前的工作。因此\((J,C)\)在\(S\)中形成不稳定对,所以\(S\)不是稳定的。我们得出了与\(S\)存在且\(C\)和\(J\)未配对相矛盾的结论。 因此,如果工作\(J\)和候选人\(C\)将对方放在各自偏好列表的首位,那么在每个稳定配对中\(J\)必须与\(C\)配对。
- 假:关键是要意识到如果工作\(J\)和候选人\(C\)也在其他人的偏好列表底部,这是可能的。例如,一个有两个工作和两个候选人的实例,其中第一个工作对两个候选人都是最好的,并且第一个候选人对两个工作都是最好的,其唯一稳定配对是第一个工作和第一个候选人配对(根据(b)部分),第二个工作和第二个候选人配对。第二个工作和第二个候选人是彼此最不喜欢的选择。
- 真:这个解决方案的关键思想是我们想要一组偏好,使得\(J_i\)和\(C_i\)彼此最不喜欢并且将\(J_i\)和\(C_i\)配对在一起。在这个匹配\(M\)中,每个未匹配的对都是不稳定对。特别是,可以通过形成偏好来构造一个实例,其中工作\(i\)(候选人\(i\))最不喜欢的候选人是候选人\(i\)(工作\(i\)),并且对所有其他候选人有任意排序。因此,对于任何工作\(i\)和候选人\(j\)(\(i\neq j\)),工作\(i\)更喜欢候选人\(j\)胜过\(i\)(其在\(M\)中的伙伴),并且候选人\(j\)更喜欢工作\(i\)胜过\(j\)(其在\(M\)中的伙伴)。也就是说,每对\(i\)和\(j\)都是不稳定对。 一个有两个工作和两个候选人的例子是以下实例:
| 工作 | 候选人 | ||||
|---|---|---|---|---|---|
| 1 | A | B | \(A\) | 1 | 2 |
| 2 | B | A | \(B\) | 2 | 1 |
配对\(P = \{(A,2),(B,1)\}\)是这样一个配对,其中不在\(P\)中的每对工作和候选人,\((A,1)\)和\((B,2)\),都是不稳定对。
4. 稳定匹配 III
- 真还是假?
- 如果候选人在某一天不小心拒绝了他们更喜欢的工作,那么算法仍然总是以一个匹配结束。
- 求婚与拒绝算法从不产生候选人最优匹配。
- 如果同一个工作在每个候选人的偏好列表中都排在最后,那么这个工作必须最终与它最不喜欢的候选人配对。
- 正如你在课堂上学到的,工作求婚的求婚与拒绝算法产生一个雇主最优稳定匹配。让我们看看候选人是否有任何方法来提高他们的地位。假设恰好有一个候选人有权力任意拒绝一个求婚,无论他们的候选名单上有哪个工作(如果有的话)。构造一个例子来说明以下情况:对于任何\(n\geq2\),存在一个稳定匹配实例,对于该实例,使用这种权力有助于每个候选人,即每个候选人都得到比在工作求婚的求婚与拒绝算法下更好的工作。
解决方案:
- 假,考虑以下情况:
| 工作 | 候选人 |
|---|---|
| 1 | \(A > B\) |
| 2 | \(B > A\) |
| 候选人 | 工作 |
|---|---|
| \(A\) | \(1 > 2\) |
| \(B\) | \(2 > 1\) |
使用 SMA(求婚与拒绝算法),匹配将是\((A,1),(B,2)\)。如果候选人\(A\)尽管候选名单上没有其他工作却拒绝了工作\(1\),工作\(1\)将向候选人\(B\)求婚并也被拒绝。这使得候选人\(A\)和工作\(1\)都没有伙伴。在这种情况下,意外的拒绝完全阻止了匹配的产生。
- 假。假设所有工作都有不同的第一选择。还假设工作求婚是每个候选人的第一选择。在这种情况下,算法在第一天结束后,工作和候选人都将得到他们的首选。在这种情况下,结果是候选人最优的。
- 假,考虑以下实例,其中工作是数字,候选人是字母:
| 工作 | 候选人 |
|---|---|
| 1 | \(A > B\) |
| 2 | \(B > A\) |
| 候选人 | 工作 |
|---|---|
| \(A\) | \(2 > 1\) |
| \(B\) | \(2>1\) |
工作\(1\)在每个候选人的列表中都排在最后,然而,\(\{(A,1),(B,2)\}\)是一个稳定配对,其中工作\(1\)得到了它的首选候选人。
- 不失一般性,假设候选人\(1\)是具有这种特殊权力的候选人。现在,假设偏好列表按如下顺序排列:
| 工作 | 偏好 | 候选人 | 偏好 |
|---|---|---|---|
| 1 | \(1 > 2 > \cdots > n - 1 > n\) | 1 | \(n > n - 1 > \cdots > 2 > 1\) |
| 2 | \(2 > 3 > \cdots > n - 1 > n > 1\) | 2 | \(1 > n > n - 1 > \cdots > 2\) |
| 3 | \(3 > 4 > \cdots > n > 1 > 2\) | 3 | \(2 > 1 > n > n - 1 > \cdots > 3\) |
| \(n\) | \(n > 1 > 2 > \cdots > n - 1\) | \(n\) | \(n - 1 > n - 2 > \cdots > 1 > n\) |
如果使用这些偏好列表运行求婚与拒绝算法,那么每个候选人都将被困在他们最不喜欢的工作中。然而,假设候选人\(1\)在第一天拒绝工作\(1\),即使他们的候选名单上没有人。然后,工作\(1\)将被迫向其第二选择,候选人\(2\)求婚,他们将接受,因为这个工作是他们的第一选择。现在,工作\(2\)没有伙伴,将向候选人\(3\)求婚,候选人\(3\)将接受,留下工作\(3\)没有伙伴。这个过程继续,直到工作\(n\)向候选人\(1\)求婚。一次拒绝导致所有候选人都得到了他们的最佳选择,而不是最差选择!
5. 度序列
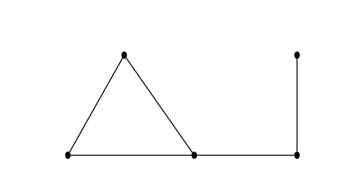
图的度序列是顶点度数的序列,按降序排列,必要时重复。例如,以下图的度序列是\((3,2,2,2,1)\)。
对于以下每个部分,确定是否存在一个简单无向图\(G\)(即没有自环和多重边的图)具有给定的度序列。证明你的说法。
- \((3,3,2,2)\)
- \((3,2,2,2,2,1,1)\)
- \((6,2,2,2)\)
- \((4,4,3,2,1)\)
解决方案:
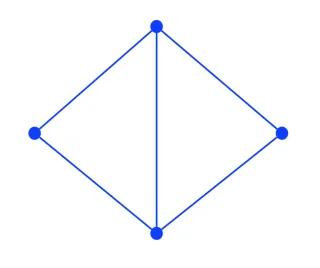
- 是 以下图有度序列\((3,3,2,2)\)。
- 否 对于任何图\(G\),具有奇数度的顶点数量是偶数(因为度数之和是边数的两倍)。给定的度序列有 3 个奇数度顶点。
- 否 顶点总数是 4。因此不可能有度数为 6 的顶点。
- 否 顶点总数是 5。因此,任何度数为 4 的顶点必须与其他每个顶点都有边相连。由于有两个度数为 4 的顶点,所以不可能有度数为 1 的顶点。
6. 构建错误?
以下“证明”有什么问题?除了找到一个反例,你还应该解释这种方法的根本错误是什么,以及为什么它展示了构建错误的危险。
错误声明:如果无向图中的每个顶点度数至少为 1,那么该图是连通的。
证明?我们对顶点数\(n\geq1\)使用归纳法。
基础情形:只有一个顶点的图只有一个,它的度数为 0。因此,基础情形是真实真空,因为前提部分为假。
归纳假设:假设对于某个\(n\geq1\)该声明为真。
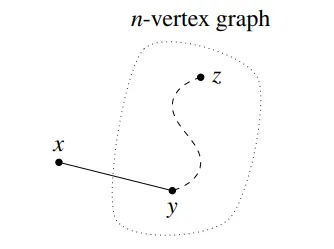
归纳步骤:我们证明对于\(n + 1\)该声明也为真。考虑一个有\(n\)个顶点且每个顶点度数至少为 1 的无向图。根据归纳假设,这个图是连通的。现在添加一个顶点\(x\)以获得一个有\((n + 1)\)个顶点的图,如下所示。
\(n\)个顶点的图
剩下的就是检查从\(x\)到其他每个顶点\(z\)是否有路径。由于\(x\)的度数至少为 1,存在从\(x\)到其他某个顶点的边;称它为\(y\)。因此,我们可以通过将边\(\{x,y\}\)连接到从\(y\)到\(z\)的路径来获得从\(x\)到\(z\)的路径。这证明了对于\(n + 1\)的声明。
解决方案:
错误在于“每个具有最小度数 1 的\((n + 1)\)个顶点的图都可以通过添加 1 个顶点从具有最小度数 1 的\(n\)个顶点的图得到”这个论点。这个证明不是从考虑任意的\((n + 1)\)个顶点的图开始,而是只考虑了可以从具有最小度数 1 的\(n\)个顶点的图开始构建的\((n + 1)\)个顶点的图。作为反例,考虑一个有四个顶点\(V = \{1,2,3,4\}\)和两条边\(E = \{\{1,2\},\{3,4\}\}\)的图。这个图中的每个顶点度数都是 1,但无法从具有最小度数 1 的 3 个顶点的图构建这个 4 个顶点的图。 更一般地说,这是归纳证明中构建错误的一个例子。通常这源于一个错误的假设,即“每个具有某种属性的大小为\(n + 1\)的图都可以从具有相同属性的大小为\(n\)的图“构建起来”。(这个假设对于某些属性是正确的,但对于其他属性,比如上面论证中的属性,是不正确的。) 避免意外构建错误的一种方法是在归纳步骤中使用“缩小、增长回来”的过程:从一个大小为\(n + 1\)的图开始,删除一个顶点(或边),将归纳假设\(P(n)\)应用于较小的图,然后添加回顶点(或边)并论证\(P(n + 1)\)成立。 让我们看看如果我们尝试用这种方法证明上面的声明会发生什么。在归纳步骤中,我们必须证明对于所有\(n\geq1\),\(P(n)\)蕴含\(P(n + 1)\)。考虑一个有\((n + 1)\)个顶点且每个顶点度数至少为 1 的图\(G\)。删除一个任意顶点\(v\),留下一个有\(n\)个顶点的图\(G'\),其中每个顶点的度数……哎呀!简化后的图\(G'\)可能包含一个度数为 0 的顶点,使得归纳假设\(P(n)\)不适用!我们被困住了——这是理所当然的,因为这个声明是错误的!
7. 欧拉回路和欧拉路径
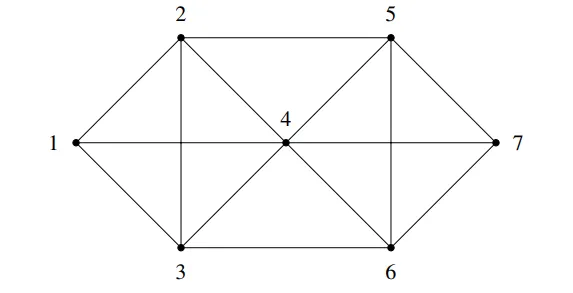
- 上面的图中有欧拉回路吗?如果没有,给出理由。如果有,提供一个例子。
- 上面的图中有欧拉路径吗?欧拉路径是一条恰好使用每条边一次的路径。如果没有,给出理由。如果有,提供一个例子。
- 无向图中有欧拉路径的条件是什么?简要证明你的答案。
解决方案:
- 否。有两个顶点的度数为奇数。
- 是。两个奇数度顶点中的一个必须是起始顶点,另一个必须是结束顶点。例如:
\[ 1\to2\to3\to4\to1\to3\to6\to4\to5\to2\to4\to7\to5\to6\to7 \]
将是一条欧拉路径(数字是按顺序访问的顶点)。注意图中有 14 条边。
- 这个解决方案很长且深入。请慢慢阅读,如果需要多次阅读也不要担心,因为这是密集的数学文本。 一个无向图有欧拉路径当且仅当它是连通的(除了孤立顶点)并且最多有两个奇数度顶点。注意不存在只有一个奇数度顶点的图(这是握手引理的结果)。欧拉回路也是一条欧拉路径,它起始和结束于同一个顶点。我们在讲座中已经看到,一个无向图\(G\)有欧拉回路当且仅当\(G\)是连通的(除了孤立顶点)并且所有顶点的度数都是偶数。我们现在将证明一个图\(G\)有一条起始和结束顶点不同的欧拉路径当且仅当它是连通的(除了孤立顶点)并且恰好有两个奇数度顶点。
证明:仅当。假设存在一条欧拉路径,比如说从\(u\)开始并在\(v\)结束(注意\(u\)和\(v\)是不同的)。那么这条路径上的所有顶点都是相互连接的,并且不在这条路径上的所有顶点(如果有的话)必须是孤立的。因此该图是连通的(除了孤立顶点)。此外,在这条路径上对一个顶点的每次中间访问都与两条边配对,因此,除了\(u\)和\(v\),所有其他顶点的度数必须是偶数。
如果。首先,注意对于一个没有奇数度顶点的连通图,我们在讲座中已经表明存在欧拉回路,这意味着存在欧拉路径。因此,让我们考虑有两个奇数度顶点的情况。
解决方案 1:取两个奇数度顶点\(u\)和\(v\),并添加一个顶点\(w\)以及两条边\((u,w)\)和\((w,v)\)。得到的图\(G'\)只有偶数度顶点(我们将\(u\)和\(v\)的度数加 1 并引入了一个度数为 2 的顶点)并且仍然是连通的。所以,我们可以在\(G'\)上找到一个欧拉回路。现在,删除使用边\((u,w)\)和\((w,v)\)的回路部分。剩下的回路部分现在是原始图上从\(u\)到\(v\)的欧拉路径,因为它遍历了原始图上的每条边。
解决方案 2:或者,我们可以构造一个与在图的笔记中描述的带拼接的\(FindTour\)算法非常相似的算法。
假设\(G\)是连通的(除了孤立顶点)并且恰好有两个奇数度顶点,比如说\(u\)和\(v\)。首先如果有孤立顶点就移除它们。由于\(u\)和\(v\)属于一个连通分量,可以找到一条从\(u\)到\(v\)的路径。考虑通过从图中移除这条路径的边得到的图。在得到的图中,所有顶点的度数都是偶数。因此,对于剩余图的每个连通分量,我们找到一个欧拉回路。(注意通过移除路径的边得到的图可能是不连通的。)观察到一条欧拉路径仅仅是覆盖所有边的边不相交的路径。我们刚刚所做的是将所有边分解为一条从\(u\)到\(v\)的路径和一堆边不相交的欧拉回路。一条路径显然是边不相交的路径。然后,给定一条边不相交的路径和一个边不相交的回路,使得它们至少共享一个公共顶点,可以通过在公共顶点处用回路扩充路径将它们组合成一条边不相交的路径。因此我们可以将所有边不相交的欧拉回路组合到从\(u\)到\(v\)的路径中,以构成从\(u\)到\(v\)的欧拉路径。
8. 给树染色
- 证明所有至少有 2 个顶点的树至少有两个叶子。回想一下,叶子被定义为树中度恰好为 1 的节点。
- 证明所有至少有 2 个顶点的树是二分图:顶点可以被分成两组,使得每条边都在两组之间。
(提示:对顶点数使用归纳法。)
解决方案:
- 对于任意一棵树\(T=(V,E)\),其中\(\vert V\vert\geq2\),假设\(L\)表示叶子的集合。这意味着我们有\(\vert V\vert-\vert L\vert\)个非叶子。叶子的度数为 1,其他顶点的度数至少为 2。此外,我们知道一个\(\vert V\vert\)个顶点的树必须有\(\vert V\vert - 1\)条边。根据握手引理,
\[ 2\vert V\vert - 2= \sum_{v\in V} \deg(v)=\sum_{v\in L}\deg(v)+\sum_{v\in V\backslash L}\deg(v)\geq\vert L\vert + 2(\vert V\vert-\vert L\vert)=2\vert V\vert-\vert L\vert \]
这意味着\(\vert L\vert\geq2\),如我们所愿。
- 对顶点数\(n\)使用归纳法证明。
基础情形\(n = 2\)。有两个顶点的树只有一条边,通过将两个顶点分成两个单独的部分,它是一个二分图。
归纳假设。假设对于任意\(k\geq2\),所有有\(k\)个顶点的树都是二分图。
归纳步骤。考虑一棵有\(k + 1\)个顶点的树\(T=(V,E)\)。我们知道每棵树必须至少有两个叶子(上一部分),所以移除一个叶子\(u\)和与\(u\)相连的边,比如说边\(e\)。得到的图\(T - u\)是一棵有\(k\)个顶点的树,根据归纳假设它是二分图。因此存在顶点的一个划分\(V = R\cup L\),使得不存在连接\(L\)中两个顶点或\(R\)中两个顶点的边。现在当我们将\(u\)加回到图中。如果边\(e\)连接\(u\)与\(L\)中的一个顶点,那么令\(L' = L\)且\(R' = R\cup\{u\}\)。另一方面,如果边\(e\)连接\(u\)与\(R\)中的一个顶点,那么令\(L' = L\cup\{u\}\)且\(R' = R\)。\(L'\)和\(R'\)给出了我们所需的划分,以表明\(T\)是二分图。这完成了归纳步骤,因此通过归纳我们得到所有至少有 2 个顶点的树都是二分图。